|
|
|
|
|
Для тех, кто хочет знать больше Дробно-линейная функция и ее графикВам известны свойства и график функции При неограниченном возрастании положительных значений аргумента значения функции, оставаясь положительными, убывают и стремятся к нулю, т. е. если х > 0 и х →+∞, то у → 0. Аналогично если х < 0 и х → -∞, то у → 0. На графике это свойство проявляется в том, что точки графика по мере их удаления в бесконечность (т. е. при х → +∞ или х → -∞) неограниченно приближаются к оси х. Говорят, что ось х, т. е. прямая у = 0, является асимптотой графика функции Вообще асимптотой кривой называется прямая, к которой приближаются как угодно близко точки кривой по мере их удаления в бесконечность. Гипербола Теперь мы познакомимся с дробно-линейными функциями. Примерами таких функций могут служить функции, задаваемые формулами Вообще дробно-линейной функцией называется функция, которую можно задать формулой вида Ограничение, что с ≠ 0 и ad - bc ≠ 0, существенно. Если с = 0, то мы получим линейную функцию, а при ad - bс = 0 — сократимую дробь, значение которой равно Вы знаете, что график функции у = ƒ(x) + n можно получить из графика функции у = ƒ(x) с помощью параллельного переноса (сдвига) вдоль оси у на n единиц вверх, если n > 0, или на -n единиц вниз, если n < 0. График функции у = ƒ(x - m) можно получить из графика функции у = ƒ(x) с помощью сдвига вдоль оси х на m единиц вправо, если m > 0, или на -m единиц влево, если m < 0. Покажем, что графиком дробно-линейной функции является гипербола, которую можно получить из гиперболы Пример 1. Построим график функции
Имеем
Здесь k = 6, m = 1, n = 2. График функции
|
|
|



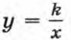 при k > 0. Отметим еще одно свойство этой функции и особенность ее графика.
при k > 0. Отметим еще одно свойство этой функции и особенность ее графика.
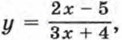
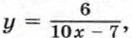
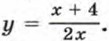 Правые части этих формул — дроби, у которых числитель — многочлен первой степени или число, отличное от нуля, а знаменатель — многочлен первой степени. Такие функции называют дробно-линейными функциями.
Правые части этих формул — дроби, у которых числитель — многочлен первой степени или число, отличное от нуля, а знаменатель — многочлен первой степени. Такие функции называют дробно-линейными функциями.
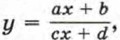 где х — переменная, а, b, с и d — произвольные числа, причем с ≠ 0 и ad - bс ≠ 0.
где х — переменная, а, b, с и d — произвольные числа, причем с ≠ 0 и ad - bс ≠ 0.
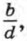 т. е. получим константу.
т. е. получим константу.
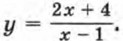
 Для этого выделим из дроби
Для этого выделим из дроби 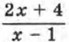 целую часть, представив дробь в виде
целую часть, представив дробь в виде 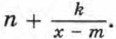
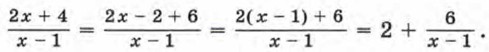
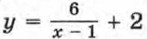 можно получить из графика функции
можно получить из графика функции 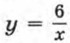 помощью двух параллельных переносов: сдвига гиперболы
помощью двух параллельных переносов: сдвига гиперболы 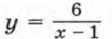 на 2 единицы вверх в направлении оси у. При этом преобразовании сдвинутся и асимптоты гиперболы
на 2 единицы вверх в направлении оси у. При этом преобразовании сдвинутся и асимптоты гиперболы