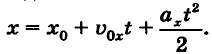|
|
|
|
|
§ 1.2. Знаковые модели Математические моделиОсновным языком информационного моделирования в науке является язык математики.
Язык математики представляет собой совокупность множества формальных языков; с некоторыми из них (алгебраическим, геометрическим) вы познакомились в школе, другие сможете узнать при дальнейшем обучении. Язык алгебры позволяет формализовать функциональные зависимости между величинами, записав соотношения между количественными характеристиками объекта моделирования. В школьном курсе физики рассматривается много функциональных зависимостей, которые представляют собой математические модели изучаемых явлений или процессов.
х = х0 + υxt. Изменение координаты тела х при прямолинейном равноускоренном движении в любой момент времени t выражается формулой:
С помощью языка алгебры логики строятся логические модели — формализуются (записываются в виде логических выражений) простые и сложные высказывания, выраженные на естественном языке. Путём построения логических моделей удаётся решать логические задачи, создавать логические модели устройств и т. д.
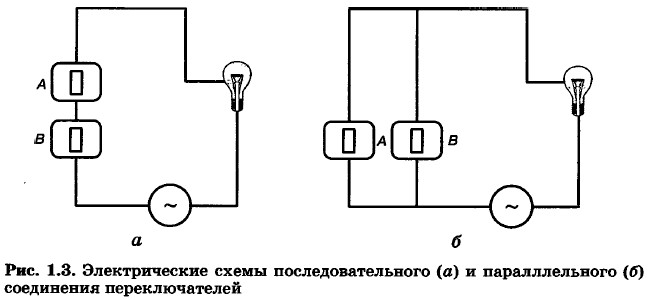
На них изображены известные вам из курса физики последовательное и параллельное соединения переключателеЗ. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателеЗ. Можно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:
Спроектируем электрическую цепь, показывающую итог таЗного голосования комиссии в составе председателя и двух рядовых членов. При голосовании «за» каждыЗ член комиссии нажимает кнопку. Предложение считается принятым, если члены комиссии проголосуют за него единогласно либо если свои голоса «за» отдадут председатель и один из рядовых членов комиссии. В этих случаях загорается лампочка. Решение. Пусть голосу председателя соответствует переключатель А, голосам рядовых членов — переключатели В и С. Тогда F(A, B,C) = A & B & C ∨ A & B ∨ A & C. Упростим полученное логическое выражение: F(A, В, С) = А & В & (С ∨ 1) ∨ A & C = A & B & 1 ∨ A & C = A & B ∨ A & C = A & (B ∨ С). Мы получили логическую модель, позволяющую построить схему проектируемой электрической цепи, изображённую на рис. 1.4.
|
|
|



 Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.
Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.
 Пример 1. Зависимость координаты тела от времени при прямолинейном равномерном движении имеет вид:
Пример 1. Зависимость координаты тела от времени при прямолинейном равномерном движении имеет вид: