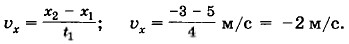Главная >> Физика 10 класс. Мякишев

Глава 1. Кинематика точки и твёрдого тела

§ 5. Примеры решения задач по теме «Равномерное прямолинейное движение»

При решении задач по данной теме необходимо прежде всего выбрать тело отсчёта и связать с ним систему координат. В данном случае движение происходит по прямой, поэтому для его описания достаточна одна ось, например ось ОХ. Выбрав начало отсчёта, записываем уравнения движения.

Задача 1. Определите модуль и направление скорости точки, если при равномерном движении вдоль оси ОХ её координата за время t₁ = 4 с изменилась от х₁ = 5 м до х₂ = -3 м.

Р е ш е н и е. Модуль и направление вектора можно найти по его проекциям на оси координат. Так как точка движется равномерно, то проекцию её скорости на ось ОХ найдём по формуле

Отрицательный знак проекции скорости означает, что скорость точки направлена противоположно положительному направлению оси ОХ. Модуль скорости υ = |υ_х| = |-2 м/с| = 2 м/с.

Задача 2. Из пунктов А и В, расстояние между которыми вдоль прямого шоссе l₀ = 20 км, одновременно навстречу друг другу начали равномерно двигаться два автомобиля. Скорость первого автомобиля υ₁ = 50 км/ч, а скорость второго автомобиля υ₂ = 60 км/ч. Определите положение автомобилей относительно пункта А спустя время t = 0,5 ч после начала движения и расстояние l между автомобилями в этот момент времени. Определите пути s₁ и s₂, пройденные каждым автомобилем за время t.

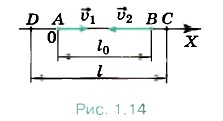
Р е ш е н и е. Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.14). Движение автомобилей будет описываться уравнениями

x₁ = х₀₁ + υ_1xt, x₂ = х₀₂ + υ_2xt.

Так как первый автомобиль движется в положительном направлении оси ОХ, а второй — в отрицательном, то υ_1x = υ₁, υ_2x = -υ₂. В соответствии с выбором начала координат х₀₁ = 0, х₀₂ = l₀. Поэтому спустя время t

x₁ = υ₁t = 50 км/ч • 0,5 ч = 25 км;

х₂ = l₀ - υ₂t = 20 км - 60 км/ч • 0,5 ч = -10 км.

Продолжение >>>