|
|
|
|
|
Глава 14. Электростатика § 93. Потенциальная энергия заряженного тела в однородном электростатическом полеВспомните из курса механики определение потенциальной энергии в поле силы тяжести. Какие силы действуют на точечный заряд в электростатическом поле? Какое поле называется однородным? Заряженные тела притягивают или отталкивают друг друга. При перемещении заряженных тел, например листочков электроскопа, действующие на них силы совершают работу. Из механики известно, что система, способная совершить работу благодаря взаимодействию тел друг с другом, обладает потенциальной энергией. Значит, система заряженных тел обладает потенциальной энергией, называемой электростатической или электрической.
Энергия взаимодействия электронов с ядром в атоме и энергия взаимодействия атомов друг с другом в молекулах (химическая энергия) — это в основном электрическая энергия. С точки зрения теории близкодействия на заряд непосредственно действует электрическое поле, созданное другим зарядом. При перемещении заряда действующая на него со стороны поля сила совершает работу. (В дальнейшем для краткости будем говорить просто о работе поля.) Поэтому можно утверждать, что заряженное тело в электрическом поле обладает энергией. Найдём потенциальную энергию заряда в однородном электрическом поле.
Работа при перемещении заряда в однородном электростатическом поле. Однородное поле создают, например, большие параллельные металлические пластины, имеющие заряды противоположного знака. Это поле действует
на заряд q с постоянной силой Пусть пластины расположены вертикально (рис. 14.31), левая пластина В заряжена отрицательно, а правая — положительно. Вычислим работу, совершаемую полем при перемещении положительного заряда q из точки 1, находящейся на расстоянии d1 от левой пластины, в точку 2, расположенную на расстоянии d2 от неё. Точки 1 и 2 лежат на одной силовой линии. Электрическое поле при перемещении заряда совершит положительную работу: А = qE(d1 - d2) = qEΔd. (14.12)
Докажем это непосредственным расчётом. Пусть перемещение заряда происходит по кривой (рис. 14.32). Разобьём эту кривую на малые перемещения. Сила, действующая на заряд, остаётся постоянной (поле однородно), а угол а между направлением силы и направлением перемещения будет изменяться. Работа на малом перемещении Δ С помощью аналогичных рассуждений можно вывести формулу для работы кулоновской силы при перемещении заряда q0 из точки 1 в точку 2 в неоднородном поле неподвижного точечного заряда q. При этом должно быть учтено, что сила
Мы видим, что работа зависит только от положения начальной (r1) и конечной (r2) точек траектории и не зависит от формы траектории. Электростатическая сила, действующая на заряды, является так же, как и силы тяжести, тяготения и упругости, консервативной силой.
Потенциальная энергия. Поскольку работа электростатической силы не зависит от формы траектории точки её приложения, сила является консервативной, и её работа согласно формуле (5.22) равна изменению потенциальной энергии, взятому с противоположным знаком: А = -(Wп2 - Wп1) = -ΔWп. (14.13) Сравнивая полученное выражение (14.12) с общим определением потенциальной энергии (14.13), видим, что ΔWп = Wп2 - Wп1 = -qEd. Считаем, что в точке 2 потенциальная энергия равна нулю. Тогда
Теперь получим формулу для потенциальной энергии заряда, находящегося в поле точечного заряда. Изменение потенциальной энергии заряда q0 при перемещении из точки 1 в точку 2 в неоднородном поле неподвижного точечного заряда q равно работе консервативной силы, взятой с обратным знаком:
Если считать, что в бесконечно удалённой точке потенциальная энергия равна нулю (при r2 → ∞ Wп2 — 0), то потенциальная энергия заряда q0 в некоторой точке, находящейся на расстоянии r от точечного заряда q, создающего поле: Отметим, что формула (14.14) подобна формуле Wп = mgh для потенциальной энергии тела. Но заряд q в отличие от массы может быть как положительным, так и отрицательным. Если поле совершает положительную работу, то потенциальная энергия заряженного тела при его свободном перемещении в поле в точку 2 уменьшается: ΔWп < 0. Одновременно согласно закону сохранения энергии растёт его кинетическая энергия. И наоборот, если работа отрицательна (например, при свободном движении положительно заряженной частицы в направлении, противоположном направлению вектора напряжённости поля Е; это движение подобно движению камня, брошенного вверх), то ΔWп > 0. Потенциальная энергия растёт, а кинетическая энергия уменьшается; частица тормозится.
Это — свойство полей консервативных сил.
Вопросы к параграфу 1. Как связано изменение потенциальной энергии заряженной частицы с работой электрического поля? 2. Чему равна потенциальная энергия заряженной частицы в однородном электрическом поле?
|
|
|



 Понятие потенциальной энергии самое сложное в электростатике. Вспомните, как нелегко было представить себе, что такое потенциальная энергия в механике. Силу мы ощущаем непосредственно, а потенциальную энергию нет. На пятом этаже дома потенциальная энергия нашего тела больше, чем на первом. Но мы это никак не воспринимаем. Различие становится понятным, если вспомнить, что при подъёме вверх пришлось совершить работу, а также если представить себе, что произойдёт при падении с пятого этажа.
Понятие потенциальной энергии самое сложное в электростатике. Вспомните, как нелегко было представить себе, что такое потенциальная энергия в механике. Силу мы ощущаем непосредственно, а потенциальную энергию нет. На пятом этаже дома потенциальная энергия нашего тела больше, чем на первом. Но мы это никак не воспринимаем. Различие становится понятным, если вспомнить, что при подъёме вверх пришлось совершить работу, а также если представить себе, что произойдёт при падении с пятого этажа.

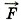 = q
= q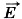 , подобно тому как Земля действует с постоянной силой
, подобно тому как Земля действует с постоянной силой 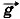 на камень вблизи её поверхности.
на камень вблизи её поверхности.

 равна ΔА = qElΔ
равна ΔА = qElΔ зависит от расстояния до точечного заряда q. Для работы кулоновской силы в поле точечного заряда q справедливо выражение
зависит от расстояния до точечного заряда q. Для работы кулоновской силы в поле точечного заряда q справедливо выражение

 Изобразите схематично однородное электрическое поле и начертите несколько траекторий, по которым движется заряд q. Покажите, что работа поля не зависит от траектории.
Изобразите схематично однородное электрическое поле и начертите несколько траекторий, по которым движется заряд q. Покажите, что работа поля не зависит от траектории.

 Потенциальная энергия прямо пропорциональна заряду q0, внесённому в поле.
Потенциальная энергия прямо пропорциональна заряду q0, внесённому в поле.
