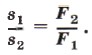|
|
|
|
|
Глава 4. Работа и мощность. Энергия § 62. Равенство работ при использовании простых механизмов. «Золотое правило» механикиРассмотренные нами простые механизмы применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу. Естественно, возникает вопрос: позволяя получить выигрыш в силе или в пути, нельзя ли с помощью простых механизмов получить выигрыш и в работе? Для ответа на поставленный вопрос проделаем опыт.
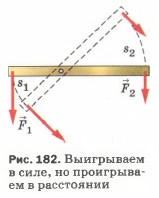
Уравновесив на рычаге две какие-нибудь разные по модулю силы F1 и F2 (рис. 182), приводят рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F2 проходит больший путь s2, а точка приложения большей силы F1 — меньший путь s1. Измерив эти пути и модули сил, находят, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:
Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути. Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу: F1S1 = F2s2, т. e. A1 = A2. Итак, при использовании рычага выигрыша в работе не получают. Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Если мы силу приложим к длинному плечу, то выиграем в силе, но во столько же раз проиграем в расстоянии. Действуя же силой на короткое плечо рычага, мы выиграем в расстоянии, но во столько же раз проиграем в силе.
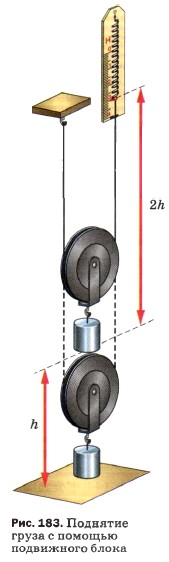
Существует легенда, что Архимед, восхищённый открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я подниму Землю!» Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали точку опоры (которая должна была бы находиться вне Земли) и рычаг нужной длины. Для подъёма Земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например со скоростью 1 м/с , потребовались бы миллионы лет. Не даёт выигрыша в работе и неподвижный блок, в чём легко убедиться на опыте (см. рис. 168). Пути, проходимые точками приложения сил F1 и F2, одинаковы, одинаковы и силы, а значит, одинаковы и работы. Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец верёвки, к которому прикреплён динамометр, как показывает опыт (рис. 183), переместить на высоту 2h. Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок не даёт выигрыша в работе. Многовековая практика показала, что ни один из механизмов не даёт выигрыша в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути. Уже древним учёным было известно правило, применимое ко всем механизмам: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики. Вопросы1. Какое соотношение существует между силами, действующими на рычаг, и плечами этих сил (см. рис. 167)?
Упражнение 331. С помощью подвижного блока груз подняли на высоту 1,5 м. На какую длину при этом был вытянут свободный конец верёвки? 2. Рабочий с помощью подвижного блока поднял груз на высоту 7 м, прилагая к свободному концу верёвки силу 160 Н. Какую работу он совершил? (Вес блока и силу трения не учитывать.) 3. Как применить блок для выигрыша в расстоянии? 4. Как можно соединить друг с другом неподвижные и подвижные блоки, чтобы получить выигрыш в силе в 4 раза; в 6 раз? 5. Решите задачу 2, учитывая вес блока, равный 20 Н. Задание
|
|
|