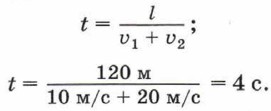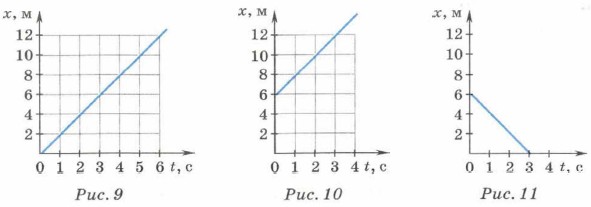
Равномерное прямолинейное движение

4. Зависимость координаты тела от времени можно представить графически.

Предположим, что тело движется из начала координат в направлении оси X с постоянной скоростью. Проекция скорости тела на эту ось равна 2 м/с. Уравнение движения в этом случае имеет вид: х = 2t (м). Зависимость координаты тела от времени — линейная. Графиком такой зависимости является прямая, проходящая через начало координат (рис. 9).

Если в начальный момент времени координата тела х₀ = 6 м, а проекция его скорости υ_x = 2 м/с, то уравнение движения имеет вид: х = 6 + 2t (м). Это тоже линейная зависимость координаты тела от времени, и её графиком является прямая, проходящая через точку, для которой при t = 0 x = 6m (рис. 10).

Рис. 11

В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: х = 6 - 2t (м). График этой зависимости представлен на рисунке 11.

Таким образом, движение тела может быть описано аналитически, т. е. с помощью уравнения движения, и графически, т. е. с помощью графика зависимости координаты тела от времени.

5. Пример решения задачи

При решении задач необходимо выполнять следующую последовательность действий.

1. Кратко записать условие задачи.

2. Проанализировать ситуацию, описанную в условии задачи:

— выяснить, можно ли принять движущиеся тела за материальные точки;

— сделать рисунок, изобразив на нём векторы скорости;

— выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.

3. Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости на координатные оси.

4. Решить задачу в общем виде.

5. Подставить в формулу значения величин и выполнить вычисления.

6. Проанализировать ответ.

Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один — со скоростью 10 м/с, другой — со скоростью 20 м/с. Определите время и координату места встречи автомобилей, если в начальный момент времени расстояние между ними равно 120 м.

Решение

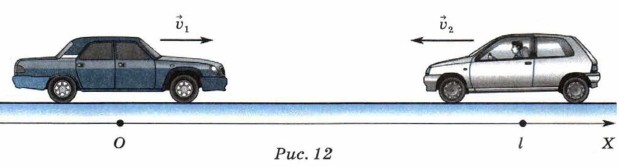
1-й способ. Свяжем систему отсчёта с Землёй, ось ОХ направим в сторону движения первого автомобиля, за начало отсчёта координаты выберем точку О — положение первого автомобиля в начальный момент времени (рис. 12).

Рис. 12

В начальный момент времени координаты каждого тела равны: х₀₁ = 0; х₀₂ = l.

Запишем уравнение движения: х = х₀ + vυ_xt.

Уравнения движения для каждого тела с учётом начальных условий имеют вид:

х₁ = υ₁t; х₂ = l - υ₂t.

В момент встречи тел х₁ = х₂, следовательно:

υ₁t = l - υ₂t.

Отсюда

Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей:

х = 10 м/с • 4 с = 40 м.

2-й способ. Построим графики зависимости координаты автомобилей от времени, соответствующие уравнениям х₁ = 10t (м) и х₂ = 120 - 20t (м) (рис. 13). Точка А пересечения графиков соответствует времени и координате места встречи автомобилей: t = 4 с, х = 40 м.

Ответ: t = 4 с; х = 40 м.

Рис. 13

<<< К началу Окончание >>>