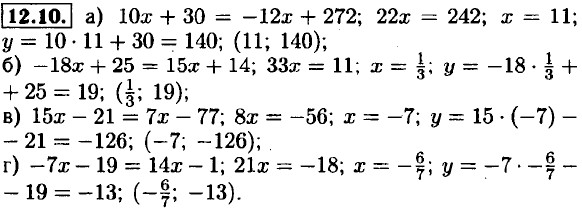Метод подстановки

12.1. а) 9х + 5 = -6х - 25; 15х = -30; х = -2; у = -2 • 9 + 5 = -13;
б) 13х - 7 = 23х - 6; 10х = 1; х = 0,1; у = 13 • 0,1 - 7 = -8,3;
в) -8х - 15 = 5х + 24; 13х = -39; х = -3; у = -3 • 5 + 25 = 9;
г) -11х + 9 = -21х + 11; 10х = 2; х = 0,2; у = -11 0,2 + 9 = 6,8.

12.2. а) 4х - (1 - 7х) = 32; 11х = 33; х = 3; у = 1 - 7 • 3 = -20;
б) 3 • (у + 2) - 2у = 9; у = 3; х = 3 + 2 = 5;
в) 5х + 2 • (х + 1) = 16; 7х = 14; х = 2; у = 2 + 1 = 3;
г) 3 • (2у - 3) + 2у = 7; 8у = 16; у = 2; х = 2 • 2 - 3 = 1.

12.3. а) 4у + 5у = 99; 9у = 99; у = 11; х = 4 • 11 = 44;
б) х - (-4х) = 10; 5х =. 10; х = 2; у = -4 • 2 = -8;
в) 4х + 6х = 150; 10х = 150; х = 15; у = 6 • 15 = 90;
г) -5у - 4у = -18; 9у = 18; у = 2; х = -5 • 2 = -10.

12.4. а) 2- 10у + 3у = 46; 23у = 46; у = 2; х = 10-2 = 20;
б) 5х + 4 • (-2,5х) = 75; -5х = 75; х = -15; у = -2,5 • (-15) = 37,5;
в) -6 • (-0,5у) - 2у = 9; у = 9; х = -0,5 • 9 = -4,5;
г) 2 • 1,5х + 5х = 64; 8х = 64; х = 8; у = 1,5 • 8 = 12.

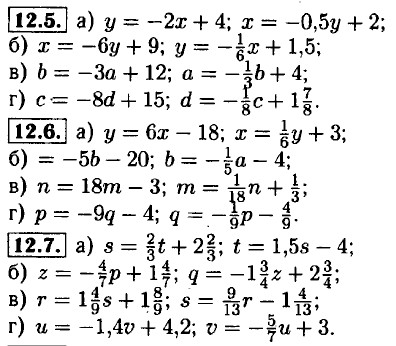
12.8. a) у = -2x + 10; 5x - 3 • (-2x + 10) = 14; 11x = 44; x = 4; у = -2 • 4 + 10 = 2;
6) x = -5y + 35; 3 • (-5y + 35) + 2y = 27; 13y - 78; у = 6; x = - 5 • 6 + 35 = 5;
в) у = -2x + 9; 7x - 2 • (-2ax + 9) = 15; 11х = 33; x = 3; у = -2 • 3 + 9 = 3;
г) x = -3у + 2; 2 • (-3у + 2) + 3у = 7; 3у = -4; у = -1x = -3 • (-1) + 2 = 5.

12.9. а) у = 2x - 2; 3x - 2 • (2x - 2) = 3; x = 1; у = 2 • 1 - 2 = 0;
б) x = 5у - 6; 3 • (5у - 6) - 4у = 4; 11у = 22; у = 2; x = 5 • 2 - 6 = 4;
в) у = 7x - 56; 3x + 4 • (7у - 56) = 55; 31x = 279; x = 9; у = 7 • 9 - 56 = 7;
г) x = 4у - 11; 6у - 2 • (4у - 11) = 13; 2у = 9; у = 4,5; x = 4 • 4,5 - 11 = 7.

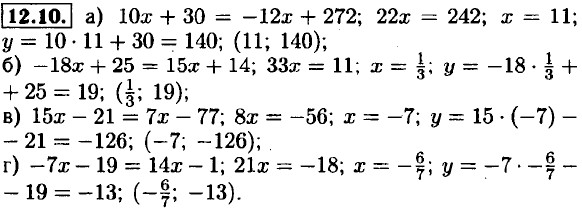
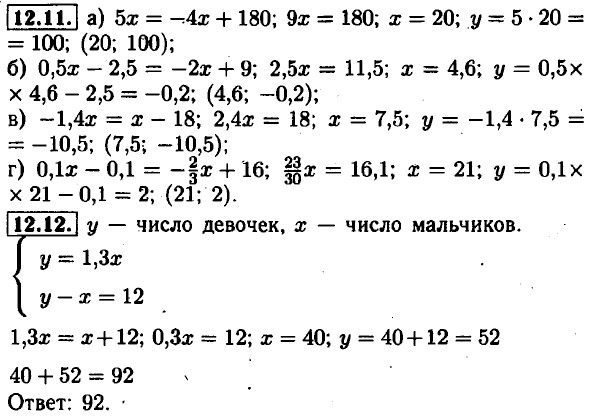
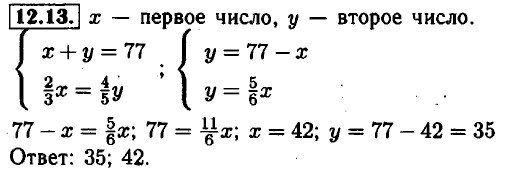
12.14. а) х = 0,75у + 3; 3 (0,75у + 3) + 4у = 34; 6,25у = 25; у = 4; х = 0,75 • 4 + 3 = 6;
б) х = 0,4у - 4; 2 • (0,4у - 4) - 5у = -8; -4,2у = 0; у = 0; х = 0,4 • 0 + 4 = 4;
в) х = 1,5у + 6; 3 • (1,5у + 6) + 2у = 5; 6,5у = -13; у = -2; х = 1,5 • (-2) + 6 = 3;
г) у = 1,25х - 1,25; 2х - 3 • (1,25х - 1,25) = 9; 1,75х = -5,25; х = -3; у = 1,25 • (-3) - 1,25 = -5.

12.15. а) х = 1,5у + 1; 4 • (1,5у + 1) - 5у = 1; у = -3; х = 1,5 • (-3) + 1 = -3,5;
б) у = -0,75х; 2х + 3 • (-0,75х) = 1; 0,25х = -1; х = -4; у = -0,75 • (-4) = 3;
в) х = 0,75у + 1,75; 5 • (0,75у + 1,75) + 2у = 26; 5,75у = 17,25; у = 3; х = 0,75 • 3 + 1,75 = 4;
г) у = 0,6x; 8 • 0,6x - 5х = -1; 0,2x = 1; х = 5; у = 0,6 • 5 = 3.

12.16. а) х = 1,75y + 8,25; 2 • (1,75 + 8,25) + 5у = 25; 8,5у = 8,5; у = 1; х = 1,75 • 1 + 8,25 = 10;
б) у = 1,2а; + 0,4; 8x - 3 • (1,2x + 0,4) = 1; 4,4x = 2,2; х = 0,5; у = 1,2 • 0,5 + 0,4 = 1;
в) х = 0,4у + 9,6; 2 • (0,4x + 9,6) + 3у = 23; 3,8у = 3,8; у = 1; х = 0,4 • 1 + 9,6 = 10;
г) х = 0,75у - 0,25; 10 • (0,75у - 0,25) - 4у = 1; 3,5у = 3,5; у = 1; х = 0,75 • 1 - 0,25 = 0,5.

12.17. а) у = -1,2x + 0,2; 2x - 3 • (-1,2x + 0,2) = 33; 5,6x = 33,6; х = 6; у = -1,2 • 6 + 0,2 = -7;
б) x = -1,2у + 0,8; 3 • (-1,2у + 0,8) + 5у = 1; 1,4у = -1,4; y = -1; х = -1,2 • (-1) + 0,8 = 2;
в) у = 0,8x + 0,4; 3х + 2 • (0,8х + 0;4) = -13; 4,6x = -13,8; х = -3; у = 0,8 • (-3) + 0,4 = -2;
г) x = -1,5у + 8; 3 • (-1,5у + 8) - 7у = 1; 11,5у = 23; у = 2; х = -1,5 • 2 + 8 = 5.

<<< К началу Решенния (окончание) >>>