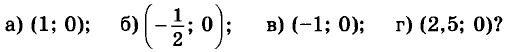|
|
Глава 7. Разложение многочленов на множители
§ 31. Вынесение общего множителя за скобки (окончание)
31.15. a) a(b - с) + 3(с - b);
б) 4(р - q) - a(q - р);
в) 6(m - n) + s(n - m);
г) 7z(x - у) - 5(y - х).
 31.16. а) (х - у)2 - а(х - у);
6) 5(а + 5)3 - (а + 3);
в) (m + n)2 + 9d(m + n);
г) (р2 - 6) - 4(р2 - 6)2.
Решите уравнение:
31.17.
|
а) х2 - 3х = 0;
б) а2 + 10а = 0;
|
в) y2 - 5у = 0;
г) b2 + 20b = 0.
|
31.18.
|
а) 0,45р2 + 18р = 0;
б) -4q2 + 3q = 0;
|
в) 9m2 + 0,27m = 0;
г) -7х2 + 2х = 0.
|
31.19.
|
а) х3 + 2х2 = 0;
б) (х - 6)2 + 2х(х - 6) = 0;
|
в) х3 - 3х2 = 0;
г) (х + 4)2 - 3х(х + 4) = 0.
|
31.20. Вычислите наиболее рациональным способом:
|
а) 1542 + 154 • 46;
б) 0,23 + 0,22 • 0,8;
|
в) 1672 - 167 • 67;
г) 0,93 - 0,81 • 2,9.
|
Разложите многочлен на множители:
31.21. а) 4с(4с - 1) - 3(4с - 1)2;
б) (а + 2)3 - 4а(а + 2);
в) 8m(m - 3) - 3(m - 3)2;
г) (а - 4)3 + 8а(а - 4).
31.22. а) а(2а - b)(а + b) - 3а(а + b)2;
б) m(3m + n2)(m - n) + mn(m - ,)2;
в) 5х2(3х - 8) + 10х(3х - 8)2;
г) 6d2(2d - 5)2 - 12d2(2d - 5)(d + 5).
31.23. Вычислите наиболее рациональным способом:
а) 0,7562 - 0,241 • 0,756 - 0,415 • 0,756;
б) 0,252 • 2,4 + 0,25 • 2,42 - 0,25 2,4 • 0,65;
в) 2,49 • 1,63 - 2,12 • 1,63 + 1,632;
г) 0,16 • 6,41 • 1,25 - 0,16 • 1,252 - 0,162 • 1,25.
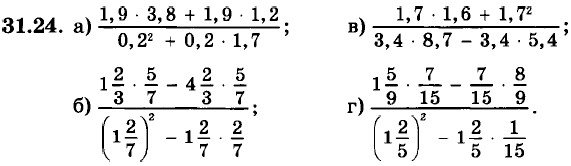
31.25. Докажите, что значение выражения:
|
а) 176 + 175 кратно 18;
б) 317 + 315 кратно 30;
|
в) 428 + 427 кратно 43;
г) 223 + 220 кратно 72.
|
 31.26. Докажите, что значение выражения:
|
а) 87 - 218 кратно 28;
б) 106 + 57 кратно 23;
|
в) 97 + 312 кратно 90;
г) 64 - 28 кратно 13.
|
31.27. Постройте график уравнения:
|
а) 2x2 + 3ху + бx = 0;
б) х2у + ху2 = 0;
|
в) 2ху - 3у2 - 6у = 0;
г) 2х2у - ху2 = 0.
|
31.28. При каких значениях р график линейной функции у = р2 - 2рх проходит через заданную точку:
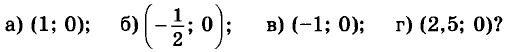
<<< К началу Решенния >>>
|