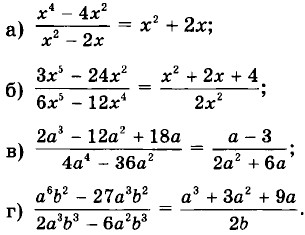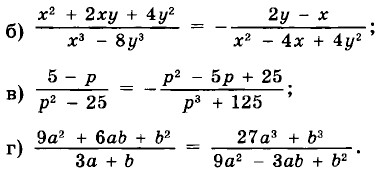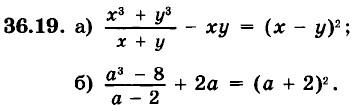|
Глава 7. Разложение многочленов на множители
§ 36. Тождества
Выясните, являются ли данные равенства тождествами:
36.1.
|
а) а + b = b + а;
б) (а + b) + с = а + (b + с);
|
в) ab = bа;
г) (аb)с = а(bс).
|
36.2.
|
а) а(b + с) = ab + ас;
б) а + 0 = а;
|
в) а • 1 = а;
г) а + (-а) = 0.
|
36.3.
|
а) а • (-5) = -аb;
б) а - b = а + (-&);
|
в) (-a)(-b) = ab;
г) а • 0 = 0.
|
Какие свойства действий позволяют утверждать, что тождественно равны выражения:
36.4. а) а + 7b и 7b + а;
б) (х + 4) + у и x + (4 + у);
в) m • 7n и 7nm;
г) 5(с + d) + 3 и 5с + 5d + 3?
36.5. а) 2с • 4 и 8с;
б) (р - p)q и 0;
в) 4t + 8sr и 8rs + 4t;
г) (а + b) • 2 и 2а + 2b?
Докажите тождество:
36.6. а) х - у = -(у - x);
б) (m - n)2 = (n - m)2;
в) 2а - 3b = -(3b - 2а);
г) (3с - 4d)2 = (4d - 3с)2.
36.7. а) 10а - (-(5а + 20)) = 5(3а + 4);
б) -(-7x) - (6 + 5x) = 2(x - 3);
в) 12у - (25 - (6у - 11)) = 18(у - 2);
г) 36 - (-(9с - 15)) = 3(3с + 7).
Докажите тождество:
36.8. а) а2 + 7а + 10 = (а + 2)(а + 5);
б) (b - 8)(b + 3) = b2 - 5b - 24;
в) х2 - 9х + 20 = (х - 4)(х - 5);
г) (с - 4)(с + 7) = с2 + 3с - 28.
 36.9. а) (а - 4)(а + 2) + 4 = (а + 1)(а - 3) - 1;
б) 16 - (х + 3)(х + 2) = 4 - (6 + х)(х - 1);
в) (у - 3)(у + 7) - 13 = (у + 8)(1y - 4) - 2;
г) (z - 11)(z + 10) + 10 = (z - 5)(z + 4) - 80.
36.10. а) (а + b)2 + (а - b)2 = 2(а2 + b2);
б) (а + b)2 - (а - b)2 = 4аb;
в) а2 + b2 = (а + b)2 - 2ab;
г) (а + b)2 - 2b(а + b) = а2 - b2.
36.11. Докажите, что выражение А + В - С тождественно равно выражению С - В - А, если А = 2x - 1, В = 3x + 1 и С = 5х.
36.12. Установите, является ли данное равенство тождеством, и если да, то укажите допустимые значения переменных:
36.13. Докажите тождество:
36.14. Докажите тождество:
а) (х + у)(х - у) + (у + а)(у - а) = (х - а)(х + а);
б) (х + а)(х + b) = х2 + (а + b)х + ab;
в) (а - b)(а + b) - (а - с)(а + с) - (с - b)(с + b) = 0;
г) (m - а)(m - b) = m2 - (а + b)m + аb.
36.15. Докажите, что если а + b = 9,
то (а + 1)(b + 1) - (а - 1)(b - 1) = 18.
36.16. Докажите, что выражение
тождественно равно нулю.
Докажите тождество:
36.17. а) (2а - b)(2а + b) + (b - с)(b + с) + (с - 2а)(с + 2а) = 0;
б) (3x + у)2 - (3х - у)2 = (3ху + 1)2 - (3ху - 1)2;
в) (х - 3у)(х + 3у) + (3у - с)(3у + с) + (с - х)(с + х) = 0;
г) (а - b)(а + b)((а - b)2 + (а + b)2) = 2(а4 - b4).
36.18. a) (а - 1)3 - 4(а - 1) = (а - 1)(а + 1)(а - 3);
б) (х2 + 1)2 - 4х2 = (х - 1)2(х + 1)2;
в) (а + 1)3 - (а + 1) = а(а + 1)(а + 2);
г) 4b2с2 - (b2 + с2 - а2)2 = (а + b + с)(а - b + с)(а + b - с)(b + с - а).
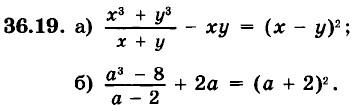
Решенния >>>
| 
