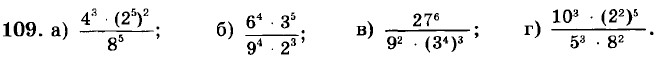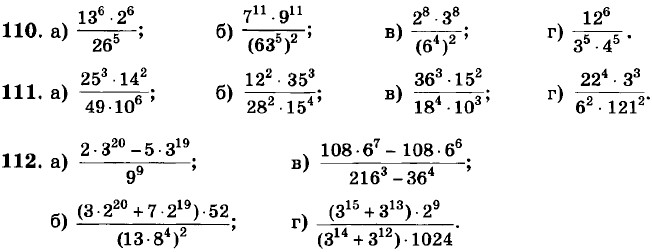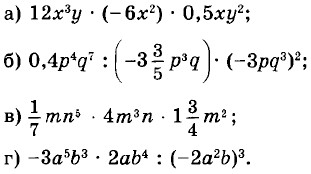Главная >> Алгебра 7 класс. Задачник с ГДЗ. Мордкович

Глава 9. Итоговое повторение

Алгебраические преобразования

Вычислите:

107. а) 3⁴ + 2⁸; б) (-1)¹⁰ - 5²; в) 3³ - 17⁰; г) 10³ - 2¹⁰.

108. а) (-2)⁶ - 5,9⁰ - 3² • 3; б) 7,4⁰ + (-2²)³ - 5⁵ : 5³; в) 7,8⁰ + ((-2)²)³ - 5³ : 5; г) 3¹³ : (3³)³ - (-2³)² + 4,7⁰.

113. Представьте в виде степени с натуральным показателем:

а) 625; б) 196; в) 81; г) 64.

114. Представьте число 256 в виде:

а) квадрата натурального числа;
б) четвёртой степени натурального числа.

115. Представьте число 729 в виде:

а) куба натурального числа;
б) квадрата натурального числа.

116. а) Представьте число 100 в виде произведения квадратов двух натуральных чисел.
б) Представьте число 216 в виде произведения кубов двух натуральных чисел.

Упростите выражение:

117.

а) а3b5 • а4b7; б) c4d7 • c8d3;

в) m9n2 • n6m3; г) p2q7 • p3q6.

118. а) (z²)⁴; б) (а⁶)²; в) (х⁵)⁶; г) (d³)³.

119. а) (а³)² • а⁵; б) (d⁴)³ • d²; в) (ƒ⁶)² • ƒ4; г) (х⁴)⁴ • х³.

120.

a) (х3у2)2 • у5 • х4; б) s5(t4)3 • (s4)6t2;

в) (k5)3l7 • k4 • (l2)8; г) а3b5 • (b2)7а4.

121.

a) (2х2)3 • (2х3)5; б) (25у4)3 : (-5y5)2;

в) (3у3)4 • (-3у4)2; г) (16х2)4 : (8х)5.

123. Преобразуйте выражение в одночлен стандартного вида и выпишите его коэффициент k:

Решите уравнение:

124. a) x⁵ = 32; б) -2x³ = 250; в) x³ = 216; г) 5x⁵ = -160.

125. a) x² = 1; б) 3x⁴ = 48; в) x⁶ = 64; г) 2x⁴ = 162.

126. a) (2x)⁷ = 128; 6) (5x)⁴ = 81; в) (3x)⁵ = 32; г) (6x)² = 144.

127. a) x³ + 1 = 0; 6) 3x⁵ + 100 = 4; в) x⁵ - 20 = 12; г) (3x)³ - 25 = 100.

128. a) 2^х = 128; б) 5^{x - 4} = 125; в) 3^х = 243; г) 6^х+1 = 216.

129. a) у^3х = 343; 6) 3^{2х - 1} = 27; в) 2^5х = 1024; г) 5^{3х + 4} = 625.

130.

a) (x + 3)3 = 1; 6) (2x - 5)5 = -243;

в) (x - 1)5 = 32; г) (5x + 4)7 = -1.

131.

a) (x + 1)8 = 256; 6) (3x - 5)4 = 81;

в) (х - 2)6 = 729; г) (7x - 2)4 = 625.

132. Стороны прямоугольника относятся как 4 : 5, а его площадь равна 180 см². Найдите стороны прямоугольника.

133. Измерения прямоугольного параллелепипеда относятся как 3 : 4 : 6, а его объём равен 576 см³. Найдите измерения прямоугольного параллелепипеда.

134. Приведите многочлен к стандартному виду:

а) х² - 2х + 4 - 2x² - 3x - 9 + х;
б) 5c²d - cd² + d³ - 2cd² + c²d - d³;
в) 12 + 3x² - 2x - x - 1 - 4x² - 7;
г) р³ + pq + pq² - q³ - р³ - q³ - pq².

135. Упростите выражение:

а) (m² - 5m + 1) - (m² - 4);
б) -3b(а - 2b) + 2а(3а - b);
в) -(9 + n²) - (6n + n² - 10);
г) у(5х - у) + 4х(х - 3у).

136. Преобразуйте произведение в многочлен стандартного вида:

а) (9 - а)(8 + а); б) (2b - 3с)(2с + 3b);

в) (15 - b)(b - 1); г) (4а - 5с)(-а + 3с).

Преобразуйте выражение в многочлен стандартного вида с помощью формул сокращённого умножения:

137. а) (а + 2)²; б) (36 - 1)²; в) (х - 8)²; г) (1 + 4у)².

138.

a) (4m + 5n)2; б) (2z - 3t)2;

в) (9р - 7q)2; г) (8r + 11s)2.

139.

a) (3x - 1)(3x + 1); б) (13m - 11n)(13m + 11n);

в) (10р + 7q)(7q - 10р); г) (4 - 5у)(5у + 4).

140. а) (х + 3)(x² - 3x + 9);
б) (2а - 3b)(4а² + баb + 9b²);
в) (х + 1)(x² - х + 1);
г) (7у² - 1)(49у⁴ + 7у² + 1).

Упростите выражение:

141. а) (1 - а)(2 + b) - (2 + а)(1 - b);
б) (2а - b)(а + b) - (а + 2b)(а - b);
в) (3 - m)(8 + n) + (m - 4)(n + 6);
г) (9m - 2n)(2m + n) - (6m + n)(3m - 2n).

142. а) (5 - x)(5 + x) + (x - 3)²;
б) b²(а + b) + (2а - b)(4а² + 2аb + b²);
в) (3а + b)² - (а + b)(а - b);
г) (у + 3)(у² - 3у + 9) - у(у² - 2).

143. Докажите тождество:

а) (х - 5)² - (х - 7)(х - 3) = 4;
б) (х + 3)(x - 3) - (х - 9)(x + 1) = 8x;
в) (х - 11)(x - 1) - (х + 6)² = -25;
г) (х + 1)(x - 4) - (х - 2)(х + 2) = -3x.

Решите уравнение:

144. а) (х + 1)(x + 2) - (х + 3)(х + 4) = 0;
б) 10х² - (2х - 3)(5х - 1) = 31;
в) (х - 2)(х - 3) - (х + 1)(х - 4) = 0;
г) 12х² - (4х - 3)(3х + 1) = - 2.

145. а) 9x² - 1 - (3х - 2)2 = 0;
б) (2х - 3)² - 2х(4 + 2х) = 11;
в) х + (5х + 2)² = 25(1 + х²);
г) (4х - 3)(3 + 4х) - 2х(8х - 1) = 0.

146. а) (2х + 3)(4х² - 6х + 9) = 0;
б) (х - 1)(х² + х + 1) = -9;
в) (3х - 1)(9х² + 3х + 1) = 0;
г) (х + 2)(х² - 2х + 4) = 7.

Окончание >>>