|
|
|
|
|
Элементы статистической обработки данных Процентные частоты. Таблицы распределения частот в процентахРяд задач данного пункта составлен с опорой на материал главы 6 «Многочлены. Операции над многочленами». Среди 19 данных b, n, а, с, а, b, b, с, n, с, d, k, b, с, d, k, с, m, а некоторого измерения результат с встретился 5 раз. Значит, частота результата с равна Например, это невозможно практически ни на одном калькуляторе. Поэтому чаще стараются иметь дело с десятичными дробями. Например,
На самом деле, с процентной частотой результата вы уже встречались ранее (см. пункты 1 и 2 Приложения), только называли её процентной долей. Правда, там ответы всегда были равны целому числу процентов, но на практике такие хорошие ответы встречаются нечасто. Результаты некоторого измерения распределены следующим образом:
П.42. а) Найдите объём и размах измерения.
П.43. а) Найдите частоту результата 7. Представьте её в виде обыкновенной дроби; в виде десятичной дроби; в процентах.
г) Перечислите те результаты, каждый из которых составляет менее 20 % общего числа результатов.
П.44. а) Какой результат встречается реже всего? Сколько раз?
П.45. а) Найдите процентную частоту наиболее редкого результата.
|
|
|



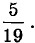 Это верный результат, но работать с таким числом не всегда удобно.
Это верный результат, но работать с таким числом не всегда удобно.
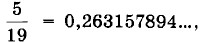 или
или 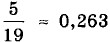 (в дальнейшем мы будем ограничиваться приближениями с точностью до тысячных, т. е. до третьего знака после запятой). В статистике, как правило, десятичные дроби умножают на 100, переводя их тем самым в проценты. В данном случае получаем, что результат с составляет примерно 26,3 % от количества всех результатов. Говорят также, что 26,3 % есть процентная частота, или частота в процентах, результата с.
(в дальнейшем мы будем ограничиваться приближениями с точностью до тысячных, т. е. до третьего знака после запятой). В статистике, как правило, десятичные дроби умножают на 100, переводя их тем самым в проценты. В данном случае получаем, что результат с составляет примерно 26,3 % от количества всех результатов. Говорят также, что 26,3 % есть процентная частота, или частота в процентах, результата с.



