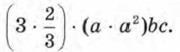|
|
|
|
|
Глава 5. Одночлены. Арифметические операции над одночленами § 20. Понятие одночлена. Стандартный вид одночленаОпределение. Одночленом называют алгебраическое выражение, которое представляет собой произведение чисел и переменных, возведённых в степень с натуральными показателями. Примеры одночленов:
Одночленами являются, в частности, также все числа, любые переменные, степени переменных. Например, одночленами являются: 0; 2; -0,6; х; а; b; х2; а3; bn (n ∈ N). Теперь приведём примеры алгебраических выражений, не являющихся одночленами:
А как вы считаете: выражение Вот ещё два примера, построенных на контрасте: Рассмотрим одночлен
Тогда, — думает математик, — я получу 2а3bс, а эта запись приятнее той, что была, хотя бы потому, что короче. Кроме того, в ней нет того сумбура, какой был сначала: первый множитель — число, второй — переменная а, затем снова число, потом опять переменная а, но уже в квадрате и т. д.». Стремящийся к чёткости, краткости и порядку математик на самом деле привёл одночлен к стандартному виду. Вообще, чтобы, привести одночлен к стандартному виду, нужно: 1) перемножить все числовые множители и поставить их произведение на первое место; 2) перемножить все имеющиеся степени с одним буквенным основанием; 3) перемножить все имеющиеся степени с другим буквенным основанием и т. д.
|
|
|



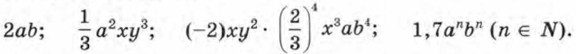
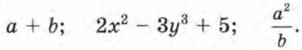

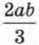 — одночлен или нет? Ведь оно по форме похоже на выражение
— одночлен или нет? Ведь оно по форме похоже на выражение 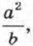 которое фигурирует у нас в числе выражений, не являющихся одночленами, и содержит в своей записи черту дроби. Тем не менее
которое фигурирует у нас в числе выражений, не являющихся одночленами, и содержит в своей записи черту дроби. Тем не менее 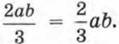
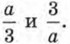 Как вы считаете, какое из этих выражений одночлен, а какое нет? А теперь проверьте себя:
Как вы считаете, какое из этих выражений одночлен, а какое нет? А теперь проверьте себя: 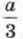 — одночлен, его можно записать в виде
— одночлен, его можно записать в виде 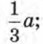 выражение
выражение 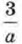 не является одночленом. Термины в математике надо употреблять правильно.
не является одночленом. Термины в математике надо употреблять правильно.
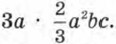 Глядя на это выражение, математик обычно рассуждает так: «От перемены мест множителей произведение не изменится, запишу-ка я это выражение в более удобном виде:
Глядя на это выражение, математик обычно рассуждает так: «От перемены мест множителей произведение не изменится, запишу-ка я это выражение в более удобном виде: