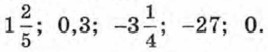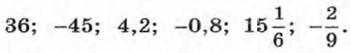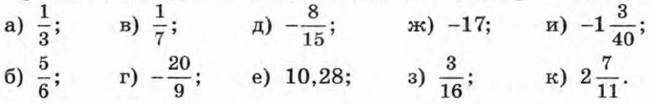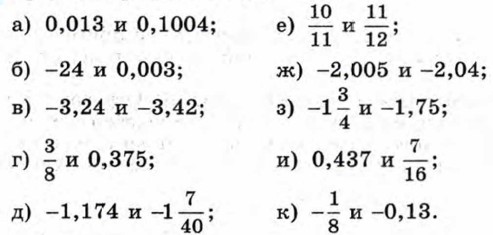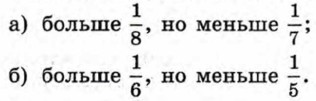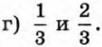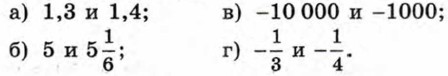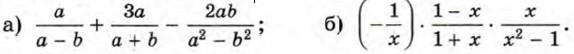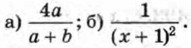Главная >> Алгебра. 8 класс. Макарычев

§ 4. Действительные числа

Рациональные числа (окончание)

Упражнения

263. Верно ли, что:

а) -4 ∈ N; -4 ∈ Z; -4 ∈ Q;
б) 5,6 ∉ N; 5,6 ∈ Z; 5,6 ∈ Q;
в) 28 ∈ N; 28 ∈ Z; 28 ∈ Q?

264. Найдите разность множеств А и В, если:

а) А — множество чётных чисел, В — множество чисел, кратных 3;
б) А — множество делителей числа 18, В — множество делителей числа 12;
в) А — множество треугольников, В — множество прямоугольных треугольников;
г) А — множество прямоугольников, В — множество ромбов.

265. Представьте в виде отношения целого числа к натуральному несколькими способами числа

266. Представьте в виде дроби с наименьшим натуральным знаменателем числа

267. Представьте в виде бесконечной десятичной дроби число:

268. Сравните рациональные числа:

269. Укажите какое-либо число, которое:

270. Укажите несколько чисел, заключённых между:

а) 10 и 10,1; б) -0,001 и 0;

в) -1001 и -1000;

271. Назовите пять чисел, заключённых между числами:

Упражнения для повторения

272. Упростите выражение:

273. Докажите, что:

а) квадрат чётного числа есть число чётное;
б) квадрат нечётного числа есть число нечётное.

274. Найдите:

а) |х|, если х = 10; 0,3; 0; -2,7; -9;
б) х, если |х| = 6; 3,2; 0.

275. Запишите без знака модуля выражение:

а) |а|, где а > 0; б) |с|, где с < 0; в) |2b|, где b < 0

Ответы

267. в) 0,(142857); г) -2,(2); д) -0,5(3); и) -1,075(0).

272.

<<< К началу