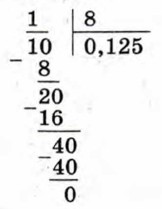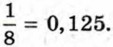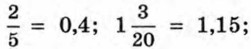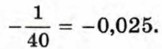|
|
|
|
|
§ 4. Действительные числа Рациональные числаВ этой главе вы узнаете, что, кроме известных вам рациональных чисел, существуют ещё иррациональные, которые вместе с рациональными числами образуют множество действительных чисел. Впервые вы встретитесь с понятием квадратного корня, узнаете, как можно находить значение квадратного корня из числа с помощью калькулятора. Вы изучите свойства корней, научитесь применять их в вычислениях и преобразованиях, познакомитесь с новой функцией у = √x, с её свойствами и графиком. Советуем обратить внимание на взаимное расположение графиков функций у = х2, где х ≥ 0, и у = √x. Вы узнаете, что графики этих функций симметричны относительно прямой у = х. В курсе математики вы встречались с различными числами. Числа 1, 2, 3, ..., которые употребляются при счёте, называются натуральными числами. Они образуют множество натуральных чисел. Натуральные числа, противоположные им числа и число нуль составляют множество целых чисел. Кроме целых, вам известны дробные числа (положительные и отрицательные). Целые и дробные числа составляют множество рациональных чисел.
Для того чтобы записать, что какое-либо число принадлежит рассматриваемому множеству, используют знак ∈. Например, утверждение, что число 2 является натуральным (или что число 2 принадлежит множеству натуральных чисел), можно записать так: 2 ∈ N. Число -2 не является натуральным; это можно записать с помощью знака ∉: -2 ∉ N. Пусть каждый элемент множества В является элементом множества А. В таких случаях множество В называют подмножеством множества А. Это записывают так: В ⊂ А (читают: В — подмножество множества А). Ведём теперь понятие разности множеств. Разностью множеств А и В называется множество, состоящее из всех элементов, которые принадлежат множеству А и не принадлежат множеству В. Например, разностью множества целых чисел Z и множества натуральных чисел N является множество, состоящее из всех целых отрицательных чисел и нуля.
Например,
Термин «рациональное число» произошёл от латинского слова ratio, что в переводе означает «отношение» (частное). Рассмотрим вопрос о представлении рациональных чисел в виде десятичных дробей. Представим в виде десятичной дроби число
Таким образом, Точно так же можно показать, что
|
|
|



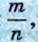 где m — целое число, а п — натуральное. Одно и то же рациональное число можно представить в таком виде разными способами.
где m — целое число, а п — натуральное. Одно и то же рациональное число можно представить в таком виде разными способами.
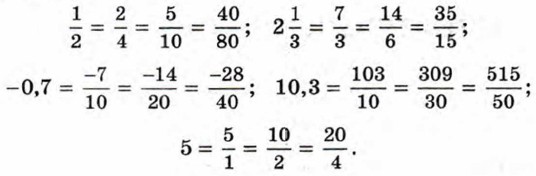
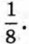 Для этого разделим числитель дроби на её знаменатель. Получим:
Для этого разделим числитель дроби на её знаменатель. Получим: