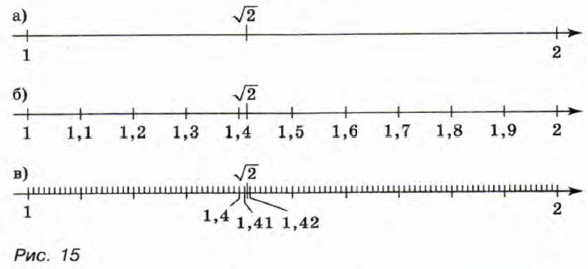
Нахождение приближённых значений квадратного корня

Рассмотрим, как можно находить приближённые значения арифметического квадратного корня.

Найдём, например, приближённое значение √2 с тремя знаками после запятой.

Так как 1² меньше 2, а 2² больше 2, то число √2 заключено между целыми числами 1 и 2 (рис. 15, а). Значит, десятичная запись числа √2 начинается так:

√2 = 1,... .

Найдём теперь цифру десятых. Для этого будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3; ..., пока не получим число, большее двух. Имеем

1,1² = 1,21; 1,2² = 1,44; 1,3² = 1,69;
1,4² = 1,96; 1,5² = 2,25.

Так как 1,4² меньше 2, а 1,5² больше 2, то число √2 больше 1,4, но меньше 1,5 (рис. 15, б). Значит,

√2 = 1,4... .

Чтобы найти цифру сотых, будем последовательно возводить в квадрат десятичные дроби 1,41; 1,42; ... . Так как 1,41² = 1,9881, а 1,42² = 2,0164, то число √2 больше 1,41 и меньше 1,42 (рис. 15, в). Значит,

√2 = 1,41... .

Продолжая этот процесс, найдём, что десятичная запись числа √2 начинается так: 1,414... . Поэтому

√2 ≈ 1,414.

Рассмотренный приём позволяет извлекать арифметический квадратный корень из числа с любой точностью. В практических расчётах для нахождения приближённых значений квадратных корней используют специальные таблицы или вычислительную технику.

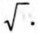Для извлечения квадратных корней с помощью калькулятора используют клавишу, на которой помещён знак Чтобы извлечь корень из некоторого числа, нужно ввести это число в калькулятор и затем нажать клавишу 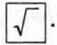На экране высветится приближённое значение корня.

Пример 1. Найдём √42,5.

Введём в калькулятор число 42,5 и нажмём клавишу со знаком На экране высветится число 6,5192024 — приближённое значение √42,5. Полученный результат округляют до требуемого числа знаков. Округлим, например, результат до сотых, получим

√42,5 ≈ 6,52.

Окончание >>>