|
|
|
|
|
§ 9. Дробные рациональные уравнения Решение задач с помощью рациональных уравненийРешение многих задач приводит к дробным рациональным уравнениям. Задача 1. Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 ч. Какова скорость лодки в стоячей воде, если скорость течения реки равна 3 км/ч?
По условию задачи на весь путь лодка затратила 2 ч. Следовательно,
Решив это уравнение, найдём его корни: x1 = 2 и х2 = 12. По смыслу задачи скорость лодки в стоячей воде должна быть больше скорости течения. Этому условию удовлетворяет второй корень — число 12 и не удовлетворяет первый. Ответ: 12 км/ч. Задача 2. К сплаву меди и цинка, содержащему 10 кг цинка, добавили 20 кг цинка. В результате содержание меди в сплаве уменьшилось на 25%. Какова была первоначальная масса сплава?
от массы сплава. Масса нового сплава, полученного после добавления 20 кг цинка, оказалась равной (х + 20) кг, а медь в нём составила
По условию задачи содержание меди уменьшилось на 25%. Следовательно,
Отсюда
Решив это уравнение, найдём, что оно имеет два корня: х1 = 20 и х2 = 40. Оба корня удовлетворяют условию задачи. Ответ: 20 кг или 40 кг. Упражнения617. Знаменатель обыкновенной дроби больше её числителя на 3. Если к числителю этой дроби прибавить 7, а к знаменателю — 5, то она увеличится на 618. Из города в село, находящееся от него на расстоянии 120 км, выехали одновременно два автомобиля. Скорость одного была на 20 км/ч больше скорости другого, и поэтому он пришёл к месту назначения на 1 ч раньше. Найдите скорость каждого автомобиля. 619. Один из лыжников прошёл расстояние в 20 км на 20 мин быстрее, чем другой. Найдите скорость каждого лыжника, зная, что один из них двигался со скоростью, на 2 км/ч большей, чем другой. 620. Два автомобиля выезжают одновременно из одного города в другой. Скорость первого на 10 км/ч больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 ч раньше второго. Найдите скорость каждого автомобиля, зная, что расстояние между городами равно 560 км.
|
|
|



 Пусть х км/ч — скорость лодки в стоячей воде. Тогда скорость лодки по течению (х + 3) км/ч, а против течения (х - 3) км/ч. По течению реки 25 км лодка прошла за
Пусть х км/ч — скорость лодки в стоячей воде. Тогда скорость лодки по течению (х + 3) км/ч, а против течения (х - 3) км/ч. По течению реки 25 км лодка прошла за 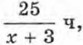 а против течения 3 км — за
а против течения 3 км — за 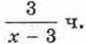 Значит, время, затраченное на весь путь, равно
Значит, время, затраченное на весь путь, равно
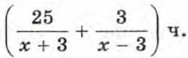
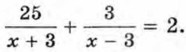

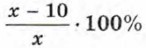
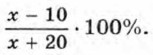
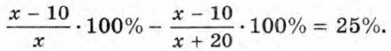
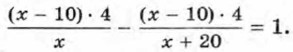
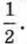 Найдите эту дробь.
Найдите эту дробь.