|
|
|
|
|
Дополнительные упражнения к главе IV Дополнительные упражнения к § 11933. Принадлежит ли промежутку [8; 41) число 40,9? Можно ли указать число, большее чем 40,9, принадлежащее этому промежутку? Существует ли в промежутке [8; 41) наибольшее число? наименьшее число? 934. Принадлежит ли промежутку (7; 17] число 7,01? Можно ли указать число, меньшее чем 7,01, принадлежащее этому промежутку? Существует ли в промежутке (7; 17] наименьшее число? наибольшее число? 935. Укажите, если это возможно, наименьшее и наибольшее числа, принадлежащие промежутку: а) [12; 37]; б) [8; 13); в) (11; 14); г) (3; 19]. 936. Верно ли, что: а) (-5; 5) ∩ (-3; 2) = (-3; 2);
937. Найдите пересечение и объединение: а) множества целых чисел и множества положительных чисел;
938. Является ли число √19 решением неравенства х √ 5? Укажите какое-нибудь число, большее √19, удовлетворяющее этому неравенству. 939. Является ли число √11 решением неравенства х > 3? Укажите какое-либо число, меньшее √11, удовлетворяющее этому неравенству. 940. Решите неравенство:
941. При каких значениях а верно неравенство:
942. Решите неравенство:
943. Найдите все натуральные числа, удовлетворяющие неравенству: а) 3(5 - 4х) + 2(14 + х) > 0; б) (х + 1)(х - 1) - (х2 - 3х) ≤ 14. 944. При каких значениях х: а) значение дроби 945. Решите неравенство: а) 2(4у - 1) - 5у < 3у + 5; б) 6(1 - у) - 8(3у + 1) + 30у > -5. 946. Найдите, при каких значениях а уравнение имеет положительный корень:
947. Найдите, при каких значениях 6 уравнение имеет отрицательный корень:
|
|
|



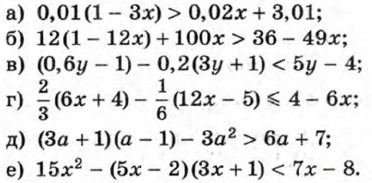
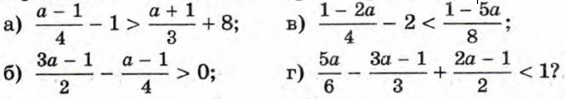
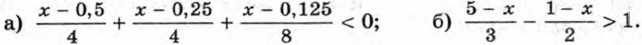
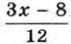 больше соответствующего значения дроби
больше соответствующего значения дроби 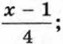
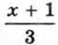 меньше соответствующего значения дроби
меньше соответствующего значения дроби