|
|
|
|
|
Сведения из курса алгебры 7 класса Уравнения (окончание)14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = -1 — решение системы Решить систему уравнений — значит найти все её решения или доказать, что решений нет. Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными. 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения. При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение: если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы; если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы. При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом: выражают из какого-либо уравнения системы одну переменную через другую; подставляют в другое уравнение системы вместо этой переменной полученное выражение; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной. При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом: умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами; складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
|
|
|



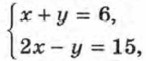 так как является верным каждое из равенств 7 + (-1) = 6 и 2 • 7 - (-1) = 15.
так как является верным каждое из равенств 7 + (-1) = 6 и 2 • 7 - (-1) = 15.