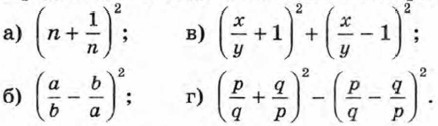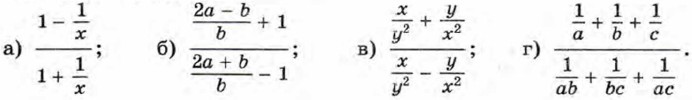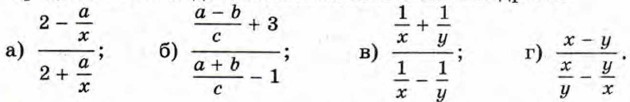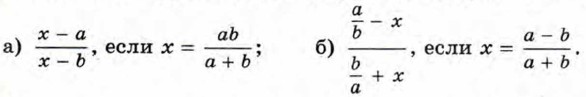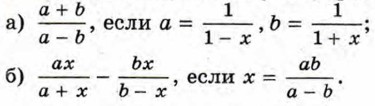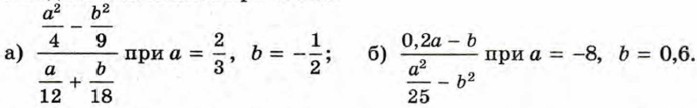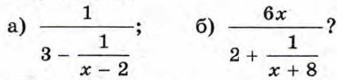|
|
|
|
|
§ 3. Произведение и частное дробей Преобразование рациональных выражений (окончание)161. Докажите, что при всех допустимых значениях переменных значение выражения не зависит от значений входящих в него переменных:
162. Докажите, что при любом натуральном n значение выражения 163. Представьте в виде многочлена или рациональной дроби:
164. Упростите выражение:
165. Представьте в виде отношения многочленов дробь:
166. Выполните подстановку и упростите полученное выражение:
167. Выполните подстановку и упростите полученное выражение:
168. Найдите значение выражения:
1) Обсудите, о каких значениях переменной х в заданиях а) и б) можно сказать сразу, что они не являются допустимыми. Что надо сделать, чтобы найти другие значения х, которые не являются допустимыми?
169. (Для работы в парах.) При каких значениях х имеет смысл выражение:
170. Найдите среднее гармоническое чисел: а) 3, 5; б) 2, 4, 8; в) 5, 10, 15, 20. 171. Из пункта А в пункт В автобус ехал со скоростью 90 км/ч. На обратном пути из-за непогоды он снизил скорость до 60 км/ч. Какова средняя скорость автобуса на всём пути следования? 172. Мастер может выполнить заказ на изготовление деталей за 4 ч, а его ученик — за 6 ч. За какое время они смогут выполнить два заказа, работая совместно? 173. Готовясь к соревнованиям, школьник трижды прошёл на лыжах одну и ту же дистанцию: сначала со скоростью 9 км/ч, затем со скоростью 12 км/ч и, наконец, со скоростью 10 км/ч. Какова была средняя скорость школьника на всём пути?
|
|
|



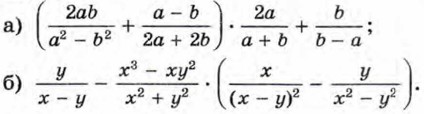
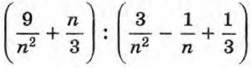 является натуральным числом.
является натуральным числом.