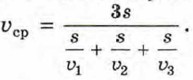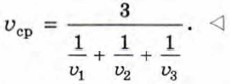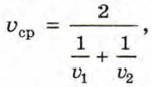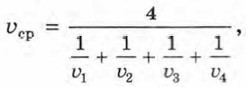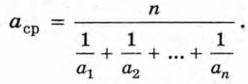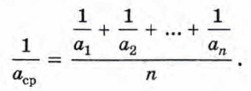|
|
|
|
|
§ 3. Произведение и частное дробей Преобразование рациональных выраженийРациональное выражение Из правил действий с дробями следует, что сумму, разность, произведение и частное рациональных дробей всегда можно представить в виде рациональной дроби. Значит, и всякое рациональное выражение можно представить в виде рациональной дроби. Пример 1. Преобразуем в рациональную дробь выражение
Запись можно вести иначе:
Пример 2. Представим выражение
в виде рациональной дроби.
Пример 3. Представим выражение
Пример 4. Пешеход отправился из посёлка А на станцию В со скоростью υ1 км/ч. Придя на станцию, он обнаружил, что оставил дома необходимые документы, и возвратился обратно в посёлок со скоростью υ2 км/ч. Взяв документы, он снова пошёл на станцию со скоростью υ3 км/ч. Выясните, какой была средняя скорость пешехода на всём пройденном им пути.
Сократив данную дробь на s, найдём, что
Мы получили формулу для вычисления средней скорости, если известны скорости υ1, υ2, υ3 на каждом из трёх участков одинаковой длины. Из полученного равенства видно, что средняя скорость движения пешехода не равна среднему арифметическому скоростей υ1, υ2 и υ3. Она вычисляется по более сложной формуле, которую называют формулой среднего гармонического трёх чисел. Средняя скорость движения на двух участках пути одинаковой длины вычисляется по формуле среднего гармонического двух чисел:
где υ1 и υ2 — скорости на этих участках. Средняя скорость движения на четырёх участках пути одинаковой длины вычисляется по формуле среднего гармонического четырёх чисел:
где υ1, υ2, υ3, υ4 — скорости на этих участках.
Эту формулу иногда записывают в другом виде:
Из этой записи видно, что величина, обратная среднему гармоническому нескольких положительных чисел, равна среднему арифметическому чисел, им обратных.
|
|
|



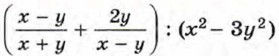 представляет собой частное от деления суммы рациональных дробей на многочлен. Деление на х2 - 3у2 можно заменить умножением на дробь
представляет собой частное от деления суммы рациональных дробей на многочлен. Деление на х2 - 3у2 можно заменить умножением на дробь 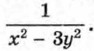 Поэтому преобразование данного выражения сводится к сложению дробей
Поэтому преобразование данного выражения сводится к сложению дробей 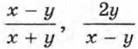 и умножению результата на дробь
и умножению результата на дробь 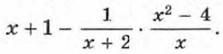
 Сначала выполним умножение дробей, затем полученный результат вычтем из многочлена х + 1:
Сначала выполним умножение дробей, затем полученный результат вычтем из многочлена х + 1:
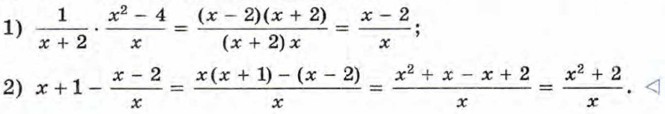
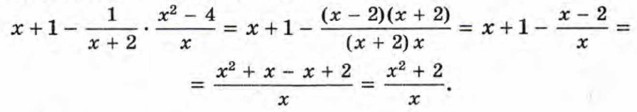
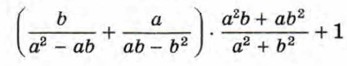
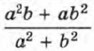 и, наконец, к полученному произведению прибавим 1:
и, наконец, к полученному произведению прибавим 1:
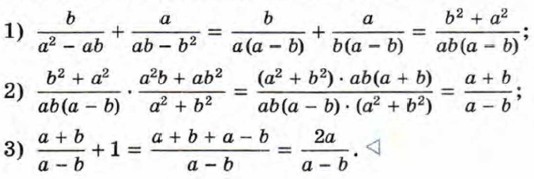
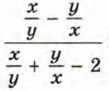 в виде рациональной дроби.
в виде рациональной дроби.
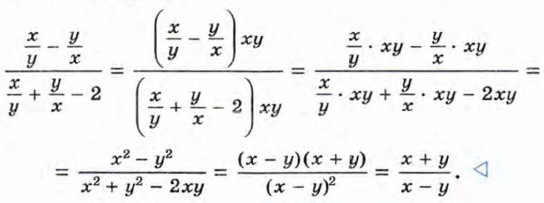
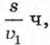 на путь от В до А —
на путь от В до А — 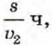 а на повторное прохождение пути от А до В —
а на повторное прохождение пути от А до В — 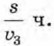
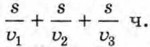 За это время он прошёл 3s км. Теперь можно найти среднюю скорость υcp пешехода на всём пути:
За это время он прошёл 3s км. Теперь можно найти среднюю скорость υcp пешехода на всём пути: