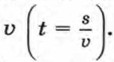|
|
|
|
|
§ 1. Функции и их свойства Функция. Область определения и область значений функцииФункция — одно из важнейших математических понятий. Напомним, что
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции. Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: у = ƒ(x) (читают: «у равно ƒ от х»). Символом ƒ(x) обозначают также значение функции, соответствующее значению аргумента, равному х. Пусть, например, функция задана формулой у = 2х2 - 6. Тогда можно записать, что ƒ(x) = 2х2 - 6. Найдем значения функции ƒ для значений х, равных 2,5 и -3: ƒ(2,5) = 2 • 2,52 - 6 = 6,5; ƒ(-3) = 2 • (-3)2 - 6 = 12. Заметим, что в записи вида у = ƒ(x) вместо ƒ употребляют и другие буквы: g, φ и т. п. Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции. Функция у = ƒ(x) считается заданной, если указана область определения функции и правило, согласно которому каждому значению независимой переменной поставлено в соответствие единственное значение зависимой переменной. Если функция у = ƒ(x) задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений переменной х, при которых выражение ƒ(x) имеет смысл. Например, областью определения функции ƒ(x) = 5х + х2 является множество всех чисел; областью определения функции Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой l = l0( 1 + αt), где l0 — начальная длина стержня, а a — коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако областью определения функции l = ƒ(t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения. Напомним, что графиком функции называется множество всех точек координатной плоскости, абсциссы, которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
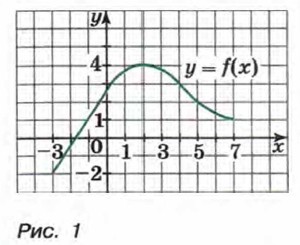
На рисунке 1 изображен график функции у = ƒ(x), областью определения которой является отрезок [-3; 7]. С помощью графика можно найти, например, что ƒ(-3) = -2, ƒ(0) = 2,5, ƒ(2) = 4, ƒ(5) = 2. Наименьшее значение функции равно -2, а наибольшее равно 4, при этом любое число от —2 до 4 является значением данной функции. Таким образом, областью значений функции у = ƒ(x) служит отрезок [-2; 4]. Мы ранее изучали некоторые важные виды функций: линейную функцию, т. е. функцию, задаваемую формулой у = kx + b, где k и b — некоторые числа; прямую пропорциональность — частный случай линейной функции, она задается формулой у = kx, где k ≠ 0; обратную пропорциональность — функцию Графиком функции у = kx + b служит прямая (рис. 2). Областью определения этой функции является множество всех чисел. Область значений этой функции при k ≠ 0 есть множество всех чисел, а при k = 0 ее область значений состоит из одного числа b.
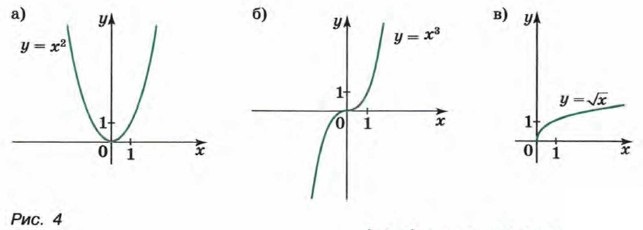
График функции Функциями такого вида описываются многие реальные процессы и закономерности. Например, прямой пропорциональностью является зависимость массы тела m от его объема V при постоянной плотности ρ (m = ρV), зависимость длины окружности С от ее радиуса R (С = 2πR). Обратной пропорциональностью является зависимость силы тока I на участке цепи от сопротивления проводника R при постоянном напряжении Мы изучали также функции, заданные формулами у = х2, у = х3, у = √х . Их графики изображены на рисунке 4.
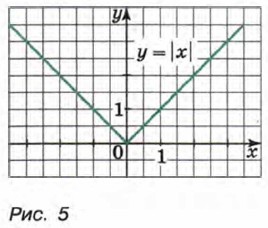
Рассмотрим еще одну функцию, а именно функцию, заданную формулой у = |х|. Так как выражение |х| имеет смысл при любом х, то областью определения этой функции является множество всех чисел. По определению |х| = х, если х ≥ 0, и |х| = -х, если х < 0. Поэтому функцию у = |х| можно задать следующим образом:
График рассматриваемой функции в промежутке [0; +∞) совпадает с графиком функции у = х, а в промежутке (—∞; 0) — с графиком функции у = -х. График функции у = |х| изображен на рисунке 5. Он состоит из двух лучей, исходящих из начала координат и являющихся биссектрисами I и II координатных углов.
|
| [an error occurred while processing this directive] |
|
|



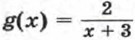 служит множество всех чисел, кроме -3.
служит множество всех чисел, кроме -3.
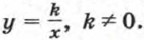
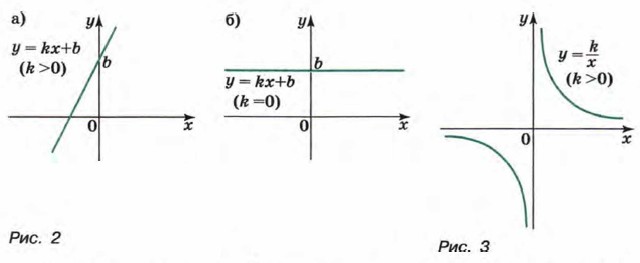
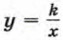 называется гиперболой. На рисунке 3 изображен график функции
называется гиперболой. На рисунке 3 изображен график функции 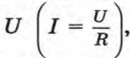 зависимость времени t, которое затрачивает равномерно движущееся тело на прохождение заданного пути s, от скорости движения
зависимость времени t, которое затрачивает равномерно движущееся тело на прохождение заданного пути s, от скорости движения