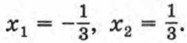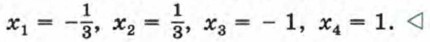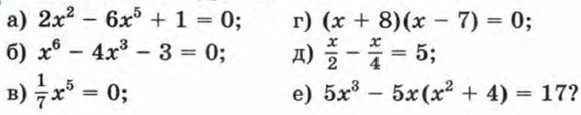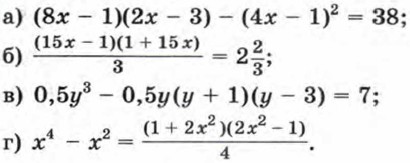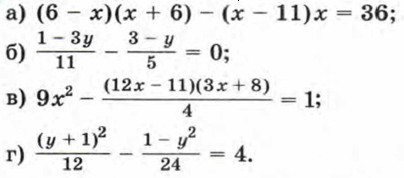|
|
|
|
|
§ 5. Уравнения с одной переменной Целое уравнение и его корни (окончание)Пример 3. Решим биквадратное уравнение 9х4 - 10х2 + 1 = 0. Введем новую переменную, обозначив х2 через у: х2 = у. Получим квадратное уравнение с переменной у: 9у2 - 10у + 1 = 0. Решив его, найдем, что
Значит,
Из уравнения
Из уравнения х2 = 1 находим, что х3 = -1, х4 = 1. Итак, исходное биквадратное уравнение имеет четыре корня:
ЭВАРИСТ ГАЛУА (1811—1832) — французский математик. Заложил основы современной алгебры, ввел ряд фундаментальных ее понятий. Нашел необходимое и достаточное условие, которому удовлетворяет алгебраическое уравнение, разрешимое в радикалах. Упражнения265. Какова степень уравнения:
266. Решите уравнение:
267. Решите уравнение:
268. Докажите, что уравнение 5х6 + 6х4 + х2 + 4 = 0 не имеет корней. 269. Может ли отрицательное число быть корнем уравнения 12х5 + 7х3 + 11х - 3 = 121? 270. Если ребро куба увеличить на 3 см, то его объем увеличится на 513 см3. Чему равно ребро куба? 271. Первое число на 5 больше второго, а его куб на 3185 больше куба второго. Найдите эти числа.
273. Решите уравнение:
274. Решите уравнение: а) х3 + 7х2 -6 = 0; б) х3 + 4х2 - 5 = 0. 275. Найдите координаты точек пересечения графика функции у = х3 - 6х2 + 11х - 6 с осями координат. 276. Решите уравнение, используя введение новой переменной: а) (2х2 + 3)2 - 12(2х2 + 3) + 11 = 0;
277. Решите уравнение: а) (x2 + 3)2 - 11(x2 + 3) + 28 = 0;
278. Решите биквадратное уравнение:
279. Найдите корни биквадратного уравнения:
|
|
|



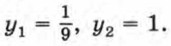
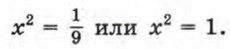
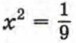 находим, что
находим, что