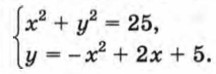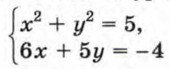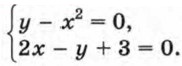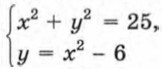Главная >> Алгебра 9 класс. Макарычев

§ 7. Уравнения с двумя переменными и их системы

Графический способ решения систем уравнений

В курсе алгебры 7 класса мы рассматривали системы уравнений первой степени с двумя переменными. Теперь займемся решением систем, составленных из двух уравнений второй степени или из одного уравнения первой, а другого второй степени.

Напомним, что пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство, называется решением системы. Решить систему — значит найти все ее решения или доказать, что решений нет.

Начнем с графического способа решения.

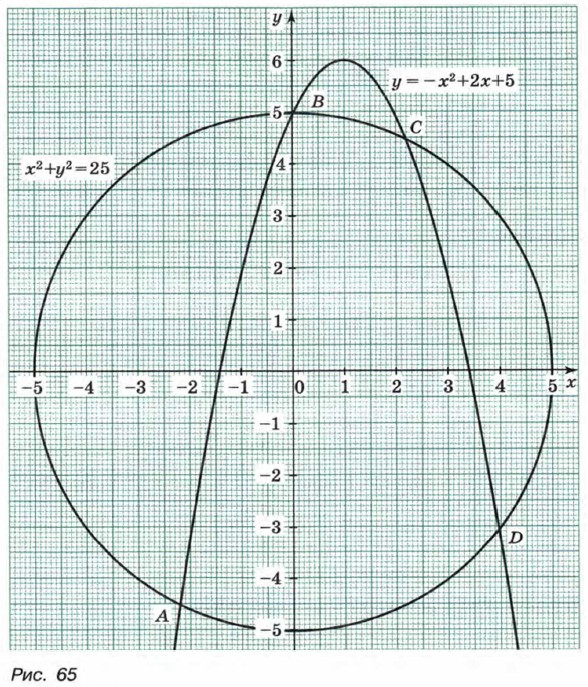
Пусть требуется решить систему уравнений

Построим в одной системе координат графики уравнений

х² + у² = 25 и у = -х² + 2х + 5

(рис. 65). Координаты любой точки окружности являются решением уравнения х² + у² = 25, а координаты любой точки параболы — решением уравнения у = -х² + 2х + 5. Значит, координаты любой точки пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, т. е. являются решением рассматриваемой системы. Используя рисунок, находим приближенные значения координат точек пересечения графиков: А(-2,2; -4,5), В(0; 5), С(2,2; 4,5), D(4; -3). Следовательно, система уравнений имеет четыре решения:

x1 ≈ -2,2, у1 ≈ -4,5; х3 ≈ 2,2, у3 ≈ 4,5;

х2 ≈ 0, у2 ≈ 5; х4 ≈ 4, у4 ≈ -3.

Подставив найденные значения х и у в уравнения системы, можно убедиться, что второе и четвертое решения являются точными, а первое и третье — приближенными.

Упражнения

415. Является ли решением системы уравнений

пара чисел: а) (-2; 1); б) (1; -2)?

416. Решите графически систему уравнений

417. Покажите с помощью графиков, что система уравнений

Окончание >>>