|
|
|
|
|
§ 7. Уравнения с двумя переменными и их системы Решение систем уравнений второй степени (окончание)439. Решите систему уравнений
сначала графическим способом, а затем аналитическим. 440. Решите систему уравнений графически и аналитически:
441. Решите систему уравнений:
442. Решите систему уравнений:
443. Решите систему уравнений:
444. Не выполняя построения: а) определите, пересекает ли парабола у = х2 - 8х + 16 прямую 2х - 3у = 0 и если да, то в каких точках;
445. Докажите, что прямая х - у = 4 имеет одну общую точку с параболой у = х2 - 5х + 5, и найдите координаты этой точки. 446. Докажите, что парабола у = 2х2 - 5х + 1 и прямая 2х + у + 3 = О не пересекаются. 447. Решите способом подстановки систему уравнений:
448. Решите систему уравнений, используя способ сложения:
449. Не выполняя построения, найдите координаты точек пересечения: а) окружности х2 + у2 = 36 и параболы у = х2 + 6;
450. При каких значениях k парабола у = х2 + 1 и прямая y = kx имеют только одну общую точку? 451. Окружность (х - 4)2 + (у - 6)2 = 25 и прямая у = кх имеют общую точку М(1; 2). Найдите координаты другой общей точки, если такая точка существует. Упражнения для повторения452. Построив схематически графики уравнений, выясните, сколько решений имеет система уравнений:
453. Решите неравенство: а) 0,2х(х - 1) - х(0,2х + 0,5) < 0,6х - 4;
454. При каких значениях х: а) трехчлен -х2 - 2х + 168 принимает положительные значения;
|
|
|



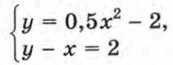
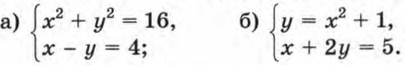
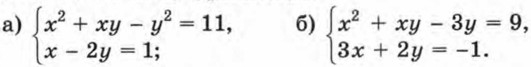
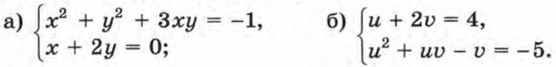
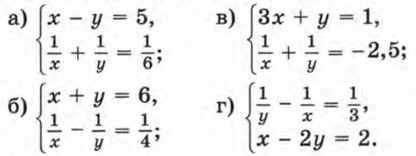
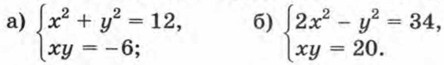
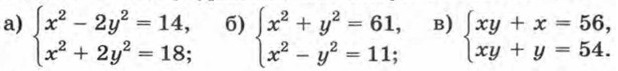
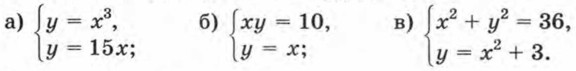
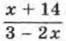 принимает отрицательные значения;
принимает отрицательные значения;
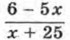 принимает положительные значения?
принимает положительные значения?