|
|
|
|
|
§ 7. Уравнения с двумя переменными и их системы Решение систем уравнений второй степениРассмотрим сначала системы уравнений с двумя переменными, составленные из одного уравнения второй степени и одного уравнения первой степени. Такую систему всегда можно решить способом подстановки. Для этого поступают следующим образом:
Пример 1. Решим систему уравнений
х = 1 - 2у. Подставим в первое уравнение вместо х выражение 1 - 2у, получим уравнение с переменной у: (1 - 2у)2 - 3(1 - 2у)у - 2у2 = 2. После упрощения получим равносильное уравнение 8у2 - 7у - 1 = 0. Решив его, найдем, что Соответствующие значения х можно найти, подставив найденные значения у в одно из уравнений системы, например во второе уравнение. Удобнее, однако, воспользоваться формулой х = 1 - 2у. Подставив в формулу х = 1 - 2у значение Подставив в формулу х = 1 - 2у значение у2 = 1, получим Итак, система имеет два решения:
Ответ можно записать также в виде пар: Если система состоит из двух уравнений второй степени с двумя переменными, то найти ее решения обычно бывает трудно. В отдельных случаях такие системы удается решить, используя способ подстановки или способ сложения. Пример 2. Решим систему уравнений
Подставим в первое уравнение вместо у выражение
Решив его, найдем, что х1 = -3, х2 = 3. По формуле у1 = 2, у2 = 2. Значит, система имеет два решения: х1 = -3, у1 = -2 и х2 = 3, у2 = 2. Ответ: (-3; -2), (3; 2).
|
|
|



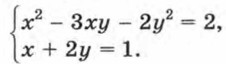
 Выразим из второго уравнения переменную х через у:
Выразим из второго уравнения переменную х через у:
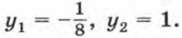
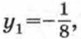 получим
получим 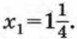
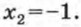
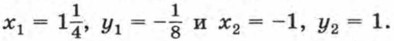
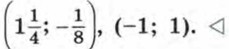
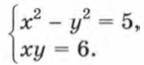
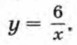
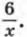 Получим уравнение
Получим уравнение
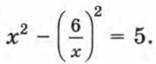
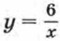 находим соответствующие значения у:
находим соответствующие значения у:
