Неравенства с двумя переменными

Рассмотрим неравенство 2х² - у < 6. При х = 2, у = 5 это неравенство обращается в верное числовое неравенство 2 • 2² - 5 < 6. Говорят, что пара (2; 5) является решением этого неравенства.

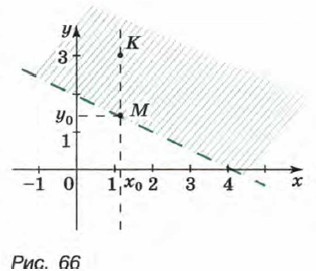
Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.

Рассмотрим, как изображается на координатной плоскости множество решений неравенства с двумя переменными.

Сначала выясним, как найти множество решений линейного неравенства с двумя переменными, т. е. неравенства вида ах + bу < с или ах + by > с, где х и у — переменные, а, b и с — некоторые числа, причем хотя бы один из коэффициентов а или b отличен от нуля.

Рассмотрим, например, неравенство х + 2у > 4 и заменим его равносильным неравенством у > -0,5л:+2. Выберем произвольно значение х, например х = 2, и найдем соответствующее ему значение выражения -0,5x + 2. Получим -0,5 • 2 + 2 = 1. Пара чисел (2; 1) является решением уравнения у = -0,5x + 2, так как ее координаты удовлетворяют этому уравнению. Любые пары чисел вида (2; у), где у > 1, например пары (2; 1,8), (2; 4), (2; 100) и т. д., являются решениями рассматриваемого неравенства. Мы нашли лишь некоторые решения неравенства у > -0,5x + 2. Чтобы найти все решения данного неравенства, будем рассуждать аналогично.

Пусть x₀ — произвольно выбранное значение х. Вычислим соответствующее ему значение выражения -0,5x+2. Получим -0,5 • х₀ + 2. Пара чисел (x₀; у₀), где у₀ = -0,5x₀ + 2, является решением уравнения у = -0,5x + 2. Тогда пары чисел (x₀; у), где у > -0,5x₀ + 2 (т. е. у > у₀), и только эти пары, образуют множество решений данного неравенства.

Теперь выясним, что представляет собой множество точек, координаты которых являются решениями неравенства х + 2у > 4. Для этого построим прямую у=-0,5х + 2, отметим на ней произвольную точку М(x₀; у₀) и проведем через нее прямую, перпендикулярную оси x (рис. 66). Координаты точки М удовлетворяют уравнению у = -0,5x+2 (так как точка М принадлежит этой прямой), а координаты любой точки К(х₀; у), где у > у₀, т. е. точки, расположенной выше точки М, удовлетворяют неравенству у > -0,5x + 2.

Значит, неравенством х+ 2у > 4 задается множество точек координатной плоскости, расположенных выше прямой у = -0,5x 2, т. е. открытая полуплоскость (полуплоскость без граничной прямой) (см. рис. 66). Чтобы показать, что прямая у = -0,5x + 2 не принадлежит полуплоскости, она на рисунке изображена штриховой линией.

Можно сделать такой вывод. Прямая х + 2у = 4 разбивает множество не принадлежащих ей точек координатной плоскости на две области: область, расположенную выше данной прямой, и область, расположенную ниже данной прямой. Координаты точек первой области удовлетворяют неравенству х + 2у > 4, а координаты точек второй области удовлетворяют неравенству х + 2у < 4.

Мы выяснили на частном примере, что представляет собой множество точек координатной плоскости, удовлетворяющих неравенствам ах + by < с и ах + by > с, в случае, когда b ≠ 0.

Рассмотрим примеры неравенств с двумя переменными второй степени.

Пример 1. Изобразим на координатной плоскости множество решений неравенства у > (х- 2)².

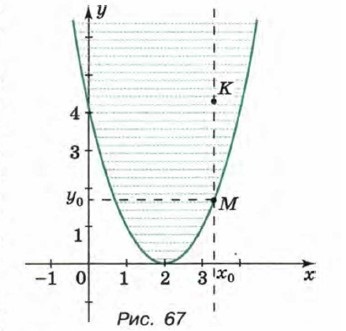
Построим график уравнения у = (х - 2)². Отметим на параболе у = (х - 2)² произвольную точку М(х₀; у₀) и проведем через эту точку перпендикуляр к оси х (рис. 67). Координаты точки М удовлетворяют уравнению у = (х - 2)², а координаты точки К(х₀; у), где у > у₀, удовлетворяют неравенству у > (х- 2)². Значит, решениями данного неравенства являются координаты точек, принадлежащих параболе у — (х — 2)², и координаты точек, расположенных выше ее. Множество решений этого неравенства изображено на рисунке 67.

Продолжение >>>