|
|
|
|
|
Дополнительные упражнения к главе IV Дополнительные упражнения к параграфу 10701. Найдите обозначенные буквами члены геометрической прогрессии (bn): а) b1; b2; 225; -135; 81; 66; ... ; б) b1; b2; b3, 36; 54; ... . 702. Последовательность (хn) — геометрическая прогрессия. Является ли геометрической прогрессией последовательность:
703. Существуют ли три числа, которые составляют одновременно арифметическую и геометрическую прогрессии? 704. Является ли геометрической прогрессией последовательность (хn), если:
705. Известны первый член и знаменатель геометрической прогрессии (bn). Найдите bn, если:
706. Первый и девятый члены геометрической прогрессии равны соответственно 135 и 707. Последовательность (6n) — геометрическая прогрессия. Докажите, что: а) если b1 > 0 и q > 1, то каждый следующий член прогрессии больше предыдущего;
Для каждого из рассмотренных случаев приведите пример. 708. Докажите, что если (аn) — геометрическая прогрессия, то: а) а2 • а6 = а3 • а5; б) аn - 3 • аn + 8 = аn • аn + 5, где n > 3. 709. Докажите, что если bn и bm — члены геометрической прогрессии, знаменатель которой равен q, то bn = bmqn - m. 710. В геометрической прогрессии (хn):
711. Сумму первых л членов последовательности (хn) можно найти по формуле 712. Геометрическая прогрессия состоит из 15 членов. Сумма первых пяти членов равна 713. Упростите выражение, применив формулу суммы первых n членов геометрической прогрессии: а) 1 + х + х2 + х3 + х4, где х ≠ 1 и х ≠ 0;
Ответы705. 710. а) х1 = 27, 711. q = 5, х1 = 3. 712. 176.
|
|
|



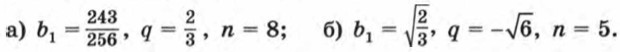
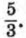 Найдите заключенные между ними члены этой прогрессии.
Найдите заключенные между ними члены этой прогрессии.
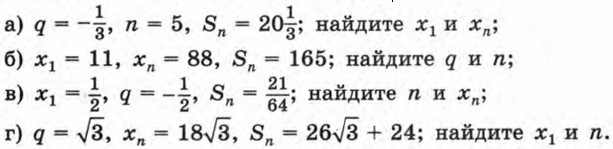
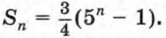 Докажите, что последовательность (хn) — геометрическая прогрессия. Найдите q и x1.
Докажите, что последовательность (хn) — геометрическая прогрессия. Найдите q и x1.
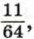 а сумма следующих пяти членов равна
а сумма следующих пяти членов равна 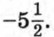 Найдите сумму последних членов этой прогрессии.
Найдите сумму последних членов этой прогрессии.
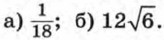
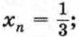 б) q = 2, n = 4; в) n = 6,
б) q = 2, n = 4; в) n = 6, 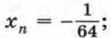 г) х1 = 2√3, n = 5.
г) х1 = 2√3, n = 5.