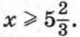|
|
|
|
|
Упражнения для повторения курса 7—9 классов Неравенства (ответы)1011. Решите неравенство:
1012. Решите неравенство: а) (2х + 1)(х 4- 4) - 3х(х + 2) < 0;
1013. Докажите, что при любых х: а) трехчлен х2 - 3х + 200 принимает положительные значения;
1014. Решите систему неравенств:
1015. Найдите целые решения системы неравенств:
1016. При каких значениях х имеет смысл выражение:
1017. Найдите область определения каждого из выражений:
Ответы1001. а) m > -4; б) х >-1,2; в) а ≤ 16; г) b ≥ 4; д) х < 0,1; е) m > -4; ж) у ≤ 10; з) а ≤ -0,5. 1002. а) х < 3; б) а > -1,5; в) у ≥ 0,16; 1003. а) При b > -62; б) при b < -0,76. 1004. а) (-∞; 2,5); 1005. а) (1; 3); б) решений нет; 1006. а) (-3; 0); б) решений нет. 1007. а) (-5,5; 1); б) (4; +∞); в) (-29; 3); г) решений нет. 1008. а) -3; -2; -1; 0; б) 2; 3; 4; 5; 6; 7. 1009. а) (-3; 6); б) [-27; -7]; в) [6; 8); г) [-0,56; 1,2]. 1010. а) При 0 ≤ ж ≤ 5; б) -17 ≤ х ≤ 13. 1011. а) (-5; 3); 1012. а) (-∞; -1) ∪ (4; +∞); б) (-∞; +∞); в) (-13; -1); г) (-4; 7). 1014. а) [-1; 2,5]; б) (-∞; 2] ∪ [3; 4,5]; в) 3; г) [0; +∞). 1015. а) 1; 2; 3; 5; 6; б) 2; 3; 4. 1016. а) При 1017. а) x — любое число; х ≠ 2,5; х ≥ 2,5; б) х — любое число; х ≠ -4 и х ≠ 0,5; х < -4 и х> 0,5; в) х — любое число; х — любое число, х — любое число.
|
|
|



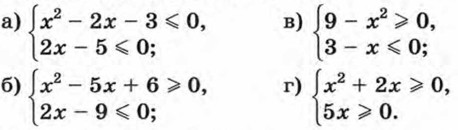
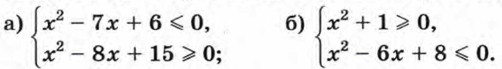
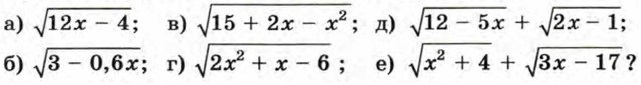
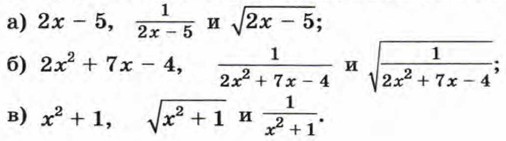
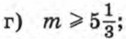 д) а >11; е) у < -0,4.
д) а >11; е) у < -0,4.
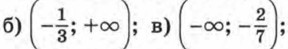 г) (-∞; -0,8).
г) (-∞; -0,8).
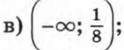 г) решений нет.
г) решений нет.
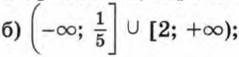
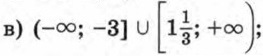 г) (-1; 1,5); д) [-0,5; 0,5]; е) (-∞; -1,2) ∪ (0; +∞); ж) (-∞; -0,2) ∪ (0,2; +∞); з) (-∞; 0) ∪ (0,8; +∞).
г) (-1; 1,5); д) [-0,5; 0,5]; е) (-∞; -1,2) ∪ (0; +∞); ж) (-∞; -0,2) ∪ (0,2; +∞); з) (-∞; 0) ∪ (0,8; +∞).
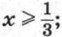 при х ≤ 5; в) при -3 ≤ х ≤ 5; г) при х ≤ -2 и х ≥ 1,5; д) при 0,5 ≤ х ≤ 2,4; е) при
при х ≤ 5; в) при -3 ≤ х ≤ 5; г) при х ≤ -2 и х ≥ 1,5; д) при 0,5 ≤ х ≤ 2,4; е) при