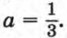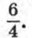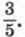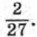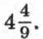|
|
|
|
|
Упражнения для повторения курса 7—9 классов Уравнения и системы уравнений (ответы)986. В арифметической прогрессии четырнадцатый член равен 140, а сумма первых четырнадцати членов равна 1050. Найдите первый член и разность этой прогрессии. 987. Последовательность (аn) — арифметическая прогрессия. Известно, что а6 = -6 и а16 = 17,5. Найдите сумму первых шестнадцати членов этой прогрессии. 988. В арифметической прогрессии первый член равен 28, а сумма первых двадцати пяти членов равна 925. Найдите разность и тридцатый член этой прогрессии. 989. В арифметической прогрессии (аn) сумма шестого и десятого членов равна 5,9, а разность двенадцатого и четвертого членов равна 2. Найдите двадцать пятый член этой прогрессии. 990. В арифметической прогрессии (аn) сумма пятого и десятого членов равна -9, а сумма четвертого и шестого членов равна -4. Найдите сумму первых десяти членов этой прогрессии. 991. В арифметической прогрессии третий член равен 150, а тринадцатый член равен 110. Сколько членов этой прогрессии, начиная с первого, сложили, если их сумма оказалась равной нулю? 992. Последовательность (хn) — геометрическая прогрессия. Найдите: а) х1, если х8 = -128 и q = -4; б) q, если х1 = 162 и х9 = 2. 993. Найдите пятый член геометрической прогрессии (bn), если известно, что b1 = 6 и 994. Найдите сумму первых шести членов геометрической прогрессии (bn), в которой 995. Пятый член геометрической прогрессии (bn) равен 996. Найдите сумму первых семи членов геометрической прогрессии (bn), если известно, что все члены последовательности положительны и b3 = 20, b5 = 80. 997. В геометрической прогрессии (bn) b1 + b2 = 30, а b2 + b3 = 20. Найдите первые три члена этой прогрессии. 998. В геометрической прогрессии (bn), знаменатель которой положителен, Ответы925. a) -4,5 б) x — любое число; в) -1; г) корней нет.
|
|
|



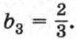
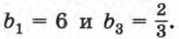
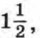 а знаменатель прогрессии равен
а знаменатель прогрессии равен 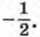 Найдите сумму первых пяти членов этой прогрессии.
Найдите сумму первых пяти членов этой прогрессии.
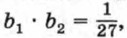 а b3 • b4 = 3. Найдите сумму первых четырех членов этой прогрессии.
а b3 • b4 = 3. Найдите сумму первых четырех членов этой прогрессии.
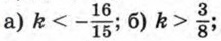 в) -2 > √5 < k < 2√5; г) таких значений k нет.
в) -2 > √5 < k < 2√5; г) таких значений k нет.
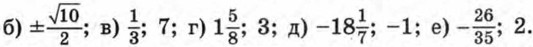
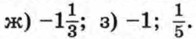
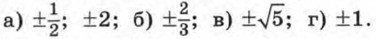
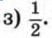
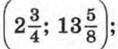 е) (1; 2),
е) (1; 2), 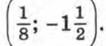
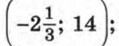 в) (-3; -5), (-5; -3), (3; 5), (5; 3); г) (-4; -2), (4; 2).
в) (-3; -5), (-5; -3), (3; 5), (5; 3); г) (-4; -2), (4; 2).