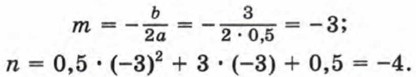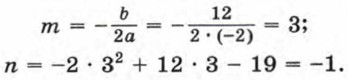|
|
|
|
|
§ 3. Квадратичная функция и ее график Построение графика квадратичной функцииДля построения графика квадратичной функции запишем формулу у = ах2 + bх + с в виде у = а(х - m)2 + n. Выделим из трехчлена ах2 + bх + с квадрат двучлена:
Отсюда Мы получили формулу вида у = а(х - m)2 + n, где Значит, график функции y = ах2 + bх + с есть парабола, которую можно получить из графика функции у = ах2 с помощью двух параллельных переносов — сдвига вдоль оси х и сдвига вдоль оси у. Отсюда следует, что график функции у = ах2 + bх + с есть парабола, вершиной которой является точка (m; n), где Осью симметрии параболы служит прямая х = m, параллельная оси у. При а > 0 ветви параболы направлены вверх, а при а < 0 — вниз.
Заметим, что абсциссу m вершины удобно находить по формуле у = аx2 + bх + с = а(х - m)2 + n = n. Приведем примеры построения графиков квадратичных функций. Пример 1. Построим график функции у = 0,5x + 3х + 0,5.
Значит, вершина параболы — точка (-3; -4). Составим таблицу значений функции:
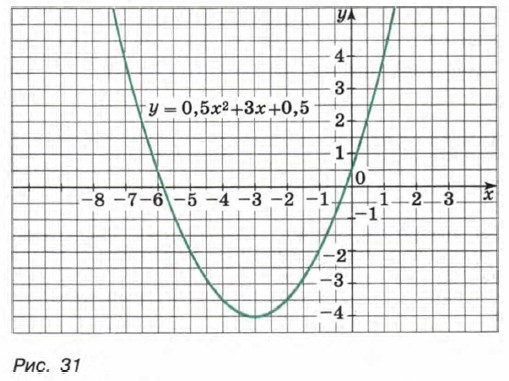
Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции у = 0,5x2 + 3х + 0,5 (рис. 31).
При составлении таблицы и построении графика учитывалось, что прямая х = -3 является осью симметрии параболы. Поэтому мы брали точки с абсциссами -4 и -2, -5 и -1, -6 и 0, симметричные относительно прямой х = -3 (эти точки имеют одинаковые ординаты). Пример 2. Построим график функции у = -2х2 + 12x - 19.
Вычислив координаты еще нескольких точек, получим таблицу:
Соединив плавной линией точки, координаты которых указаны в таблице, получим график функции у = -2х2 + 12х - 19 (рис. 32).
|
|
|



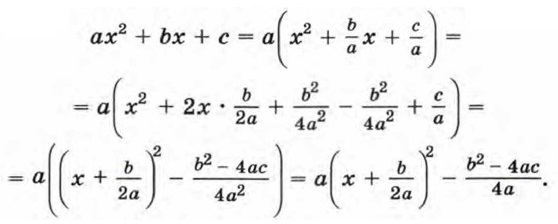
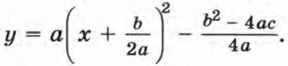
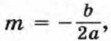
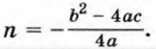
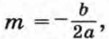
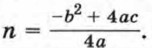
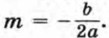 Ординату n можно находить, подставив найденное значение абсциссы в формулу у — ах2 + bх + с, так как при х = m
Ординату n можно находить, подставив найденное значение абсциссы в формулу у — ах2 + bх + с, так как при х = m
 Графиком функции у = 0,5х + 3х + 0,5 является парабола, ветви которой направлены вверх. Найдем координаты m и n вершины этой параболы:
Графиком функции у = 0,5х + 3х + 0,5 является парабола, ветви которой направлены вверх. Найдем координаты m и n вершины этой параболы: