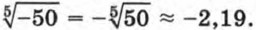|
|
|
|
|
§ 4. Корень n-й степени Корень n-й степениНапомним, что квадратным корнем из числа а называется такое число, квадрат которого равен a. Аналогично определяется корень любой натуральной степени n.
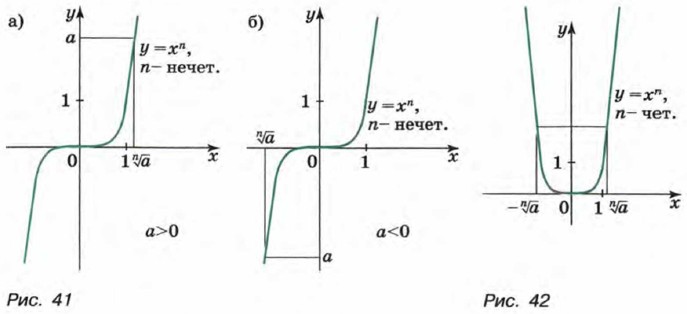
Например, корнем пятой степени из 32 является число 2, так как 25 = 32; корнем четвертой степени из 81 является каждое из чисел 3 и -3, так как 34 = 81 и (-3)4 = 81. Корень второй степени принято называть квадратным корнем, а корень третьей степени — кубическим корнем. Рассмотрим степенную функцию у = хn с нечетным показателем n (рис. 41). Для любого числа а существует единственное значение х, n-я степень которого равна а. Это значение является корнем n-й степени из а. Для записи корня нечетной степени n из числа а используют обозначение
Приведем примеры. Запись Рассмотрим теперь степенную функцию у = хn с четным показателем n (рис. 42). При любом а > 0 существуют два противоположных значения х, n-я степень которых равна а. При а = 0 такое число одно (число 0), при а < 0 таких чисел нет. Другими словами, если n — четное число и а > 0, то существует два корня n-й степени из а. Эти корни являются противоположными числами. Если а = 0, то корень n-й степени из а равен нулю. Если а < 0 и n — четное число, то корня n-й степени из а не существует. Например, запись Если n = 2, то показатель корня не пишется. Итак, если n— нечетное число, то выражение если n — четное число, то выражение Из определения корня n-й степени следует, что при всех значениях а, при которых выражение Выражение
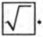
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень. Например, Вообще при любом нечетном л и положительном а верно равенство Вы знаете, что для нахождения с помощью калькулятора приближенного значения квадратного корня используется специальная клавиша Корень n-й степени из положительного числа находят с помощью калькулятора, используя клавиши Программа вычисления корня n-й степени из положительного числа а выглядит так:
Например, чтобы найти
В результате получим, что Для того чтобы найти с помощью калькулятора значение выражения
Округляя результат до 0,01, получим, что
|
|
|



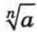 (читают: «Корень n-й степени из а»). Число n называют показателем корня, выражение, стоящее под знаком корня, — подкоренным выражением.
(читают: «Корень n-й степени из а»). Число n называют показателем корня, выражение, стоящее под знаком корня, — подкоренным выражением.
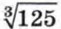 означает кубический корень из 125. Из определения корня следует, что
означает кубический корень из 125. Из определения корня следует, что 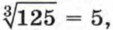 так как 53 = 125. Запись
так как 53 = 125. Запись 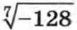 означает корень седьмой степени из -128. Так как -128 = (-2)7, то
означает корень седьмой степени из -128. Так как -128 = (-2)7, то 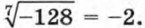
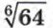 означает неотрицательный корень шестой степени из 64. Имеем
означает неотрицательный корень шестой степени из 64. Имеем 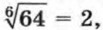 так как 2 — неотрицательное число и 26 = 64.
так как 2 — неотрицательное число и 26 = 64.
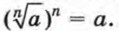
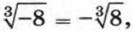 так как
так как 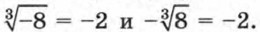
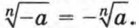
 Для корней n-й степени, где n >2, подобных клавиш нет. При нахождении корня n-й степени из положительного числа а используется принятое в математике представление выражения
Для корней n-й степени, где n >2, подобных клавиш нет. При нахождении корня n-й степени из положительного числа а используется принятое в математике представление выражения 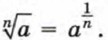
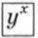 и
и 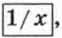 первая из которых обозначает степень, а вторая — число, обратное х.
первая из которых обозначает степень, а вторая — число, обратное х.
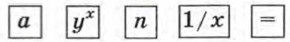
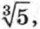 надо выполнить такую последовательность действий:
надо выполнить такую последовательность действий:

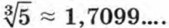
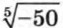 с точностью до 0,01, найдем сначала
с точностью до 0,01, найдем сначала 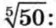

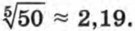 Отсюда находим, что
Отсюда находим, что