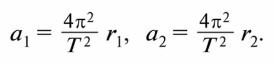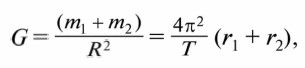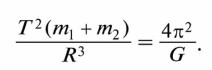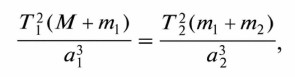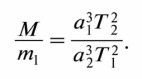|
|
|
|
|
§ 14. Движение небесных тел под действием сил тяготения Масса и плотность ЗемлиБолее точная формула третьего закона Кеплера, которая была получена Ньютоном, даёт возможность определить одну из важнейших характеристик любого небесного тела — массу. Выведем эту формулу, считая (в первом приближении) орбиты планет круговыми. Пусть два тела, имеющие массы m1, и m2, взаимно притягивающиеся и обращающиеся вокруг общего центра масс, находятся от центра масс на расстоянии r1 и r2 и обращаются вокруг него с периодом Т. Расстояние между их центрами R = r1 + r2. На основании закона всемирного тяготения ускорение каждого из этих тел равно:
Угловая скорость обращения вокруг центра масс составляет
Приравняв полученные для ускорений выражения, выразив из них r1, и r2 и сложив их почленно, получаем:
откуда
Поскольку в правой части этого выражения находятся только постоянные величины, оно справедливо для любой системы двух тел, взаимодействующих по закону тяготения и обращающихся вокруг общего центра масс, — Солнце и планета, планета и спутник. Определим массу Солнца, для этого запишем выражение:
где М — масса Солнца; m1 — масса Земли; m2 — масса Луны; Т1 и a1 — период обращения Земли вокруг Солнца (год) и большая полуось её орбиты; Т2 и а2 — период обращения Луны вокруг Земли и большая полуось лунной орбиты. Пренебрегая массой Земли, которая ничтожно мала по сравнению с массой Солнца, и массой Луны, которая в 81 раз меньше массы Земли, получим:
Подставив в формулу соответствующие значения и приняв массу Земли за единицу, мы получим, что Солнце примерно в 333 тыс. раз по массе больше нашей планеты. Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они оказывают на движение астероидов, комет или космических аппаратов, пролетающих в их окрестностях. Об определении массы звёзд см. в § 23.
|
|
|



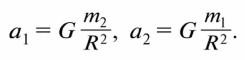
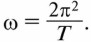 Тогда центростремительное ускорение выразится для каждого тела так:
Тогда центростремительное ускорение выразится для каждого тела так: