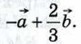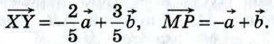|
|
|
|
|
IX. Векторы Дополнительные задачи к главе IX. Векторы800. Докажите, что если векторы 801. Докажите, что для любых векторов 802. На стороне ВС треугольника АВС отмечена точка N так, что BN = 2NC. Выразите вектор 803. На сторонах MN и NP треугольника MNP отмечены соответственно точки X и Y так, что 804. Основание AD трапеции ABCD в три раза больше основания ВС. На стороне AD отмечена такая точка К, что 805. Три точки А, В и С расположены так, что
806. Точка С делит отрезок АВ в отношении m : n, считая от точки А. Докажите, что для любой точки О справедливо равенство
807. Отрезки АА1, ВВ1 и СС1 — медианы треугольника АВС, О — произвольная точка. Докажите, что
808.* Точки А и С — середины противоположных сторон произвольного четырёхугольника, а точки В и D — середины двух других его сторон. Докажите, что для любой точки О верно равенство
809. Один из углов прямоугольной трапеции равен 120°. Найдите её среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равны а. 810. Докажите, что вершина угла, образованного биссектрисами двух углов трапеции, прилежащих к боковой стороне, лежит на прямой, содержащей среднюю линию трапеции. Ответы к дополнительным задачам главы IX801. Указание. Если векторы 802. 803. 804. 809. 810. Указание. Воспользоваться теоремой п. 74.
|
|
|



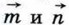 сонаправлены, то
сонаправлены, то 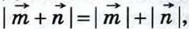 а если
а если 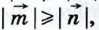 то
то 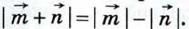
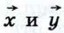 справедливы неравенства
справедливы неравенства 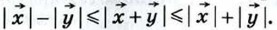
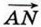 через векторы
через векторы 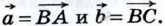
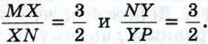 Выразите векторы
Выразите векторы 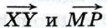 через векторы
через векторы 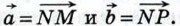
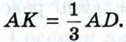 Выразите векторы
Выразите векторы 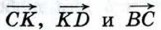 через векторы
через векторы 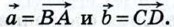
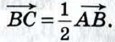 Докажите, что для любой точки О справедливо равенство
Докажите, что для любой точки О справедливо равенство
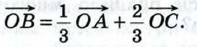
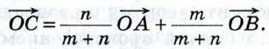
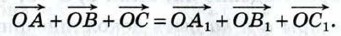
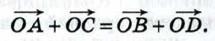
 не коллинеарны, то воспользоваться правилом треугольника сложения векторов, и если они коллинеарны — задачей 800.
не коллинеарны, то воспользоваться правилом треугольника сложения векторов, и если они коллинеарны — задачей 800.