|
|
|
|
|
Глава IX. Векторы Задачи повышенной трудности к главе IX. Векторы903 Докажите утверждения об основных свойствах умножения вектора на число (п. 86). Решение 1. Докажем, что для любых чисел k, l и любого вектора Далее, если kl ≥ 0, то 2. Докажем, что для любого числа k и любых векторов 3. Докажем, что для любых чисел k, l и любого вектора Рассмотрим вектор Следовательно, согласно определению произведения вектора на число, 904. Даны четырёхугольник MNPQ и точка О. Что представляет собой данный четырёхугольник, если 905. Даны четырёхугольник ABCD и точка О. Точки Е, F, G и Н симметричны точке О относительно середин сторон АВ, ВС, CD и DA соответственно. Что представляет собой четырёхугольник EFGH? 906. Дан треугольник АВС. Докажите, что вектор 907. Докажите следующее утверждение: три точки А, В и С лежат на одной прямой тогда и только тогда, когда существуют числа k, l и m, одновременно не равные нулю, такие, что k + 1 + m = О и для произвольной точки О выполняется равенство 908. Используя векторы, докажите, что середины диагоналей четырёхугольника и точка пересечения отрезков, соединяющих середины противоположных сторон, лежат на одной прямой. 909. Биссектрисы внешних углов треугольника АВС при вершинах А, В и С пересекают прямые ВС, СА и АВ соответственно в точках А1, В1 и С1. Используя векторы, докажите, что точки A1, В1 и C1 лежат на одной прямой. 910. Пусть Н — точка пересечения прямых, содержащих высоты неравностороннего треугольника АВС, а О — центр описанной около этого треугольника окружности. Используя векторы, докажите, что точка G пересечения медиан треугольника принадлежит отрезку НО и делит этот отрезок в отношении 2 : 1, считая от точки Н, т. е.
|
|
|



 справедливо равенство
справедливо равенство 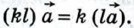 Если
Если 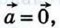 то справедливость этого равенства очевидна. Пусть
то справедливость этого равенства очевидна. Пусть 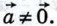 Имеем:
Имеем: 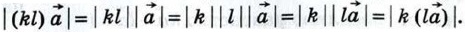
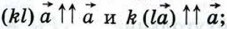 если же kl < 0, то
если же kl < 0, то 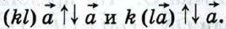 И в том и в другом случае
И в том и в другом случае 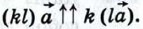 Следовательно,
Следовательно,  справедливо равенство
справедливо равенство 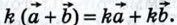 Если k = 0, то справедливость этого равенства очевидна. Пусть k ≠ 0. Рассмотрим случай, когда векторы
Если k = 0, то справедливость этого равенства очевидна. Пусть k ≠ 0. Рассмотрим случай, когда векторы 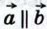 рассмотрите самостоятельно). Отложим от какой-нибудь точки О векторы
рассмотрите самостоятельно). Отложим от какой-нибудь точки О векторы 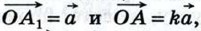 а от точек А1 и А — векторы
а от точек А1 и А — векторы 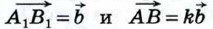 (рис. 272, а, б). Треугольники ОА1В1 и ОАВ подобны с коэффициентом подобия
(рис. 272, а, б). Треугольники ОА1В1 и ОАВ подобны с коэффициентом подобия 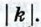 Следовательно,
Следовательно, 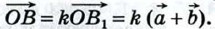 С другой стороны,
С другой стороны, 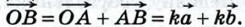 Итак,
Итак, 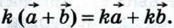
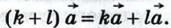 Если k = l = 0, то справедливость этого равенства очевидна. Пусть хотя бы одно из чисел k, l отлично от нуля. Для определённости будем считать, что | k | ≥ |l|, и, следовательно, k ≠ 0 и
Если k = l = 0, то справедливость этого равенства очевидна. Пусть хотя бы одно из чисел k, l отлично от нуля. Для определённости будем считать, что | k | ≥ |l|, и, следовательно, k ≠ 0 и 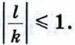
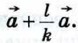 Очевидно,
Очевидно, 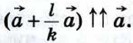 Далее,
Далее, 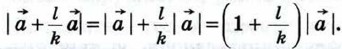
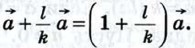 Умножая обе части этого равенства на k, получим, что справедливо равенство
Умножая обе части этого равенства на k, получим, что справедливо равенство 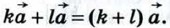
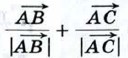 направлен вдоль биссектрисы угла А, а вектор
направлен вдоль биссектрисы угла А, а вектор 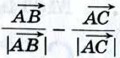 — вдоль биссектрисы внешнего угла при вершине А.
— вдоль биссектрисы внешнего угла при вершине А.