|
§ 1. Координаты вектора



Разложение вектора по двум неколлинеарным векторам
Докажем сначала лемму1 о коллинеарных векторах.
1 Леммой называется вспомогательная теорема, с помощью которой доказывается следующая теорема или несколько теорем.
Лемма
Если векторы  и и  коллинеарны и коллинеарны и 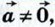 то существует такое число к, что то существует такое число к, что 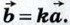
|
Доказательство
Возможны два случая: 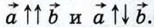 Рассмотрим эти случаи в отдельности. Рассмотрим эти случаи в отдельности.
1)  Возьмём число Возьмём число 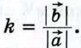 Так как k ≥ 0, то векторы Так как k ≥ 0, то векторы 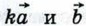 сонаправлены (рис. 273, а). Кроме того, их длины равны: сонаправлены (рис. 273, а). Кроме того, их длины равны: 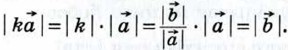 Поэтому Поэтому 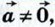
2)  Возьмём число Возьмём число 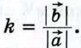 Так как k < 0, то векторы Так как k < 0, то векторы 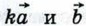 снова сонаправлены (рис. 273, б). Их длины также равны: снова сонаправлены (рис. 273, б). Их длины также равны: 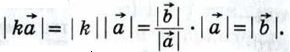 Поэтому Поэтому 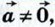 Лемма доказана. Лемма доказана.
Пусть  и и  — два данных вектора. Если вектор — два данных вектора. Если вектор 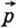 представлен в виде представлен в виде 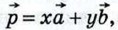 где х и у — некоторые числа, то говорят, что вектор где х и у — некоторые числа, то говорят, что вектор 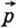 разложен по векторам разложен по векторам  и и  . Числа х и у называются коэффициентами разложения. Докажем теорему о разложении вектора по двум неколлинеарным векторам. . Числа х и у называются коэффициентами разложения. Докажем теорему о разложении вектора по двум неколлинеарным векторам.
Теорема
| На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
|
Доказательство
Пусть  и и  — данные неколлинеарные векторы. Докажем сначала, что любой вектор — данные неколлинеарные векторы. Докажем сначала, что любой вектор 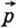 можно разложить по векторам можно разложить по векторам  и и  Возможны два случая. Возможны два случая.
Окончание >>>
| 


 и
и  коллинеарны и
коллинеарны и 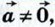 то существует такое число к, что
то существует такое число к, что 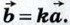
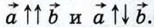 Рассмотрим эти случаи в отдельности.
Рассмотрим эти случаи в отдельности.
 Возьмём число
Возьмём число 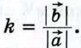 Так как k ≥ 0, то векторы
Так как k ≥ 0, то векторы 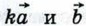 сонаправлены (рис. 273, а). Кроме того, их длины равны:
сонаправлены (рис. 273, а). Кроме того, их длины равны: 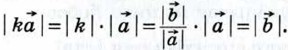 Поэтому
Поэтому  Возьмём число
Возьмём число 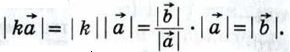 Поэтому
Поэтому 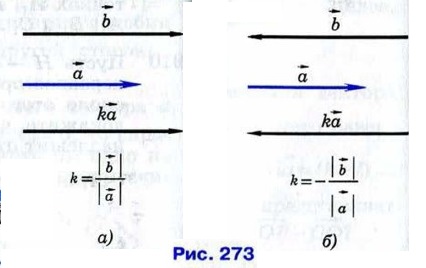
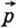 представлен в виде
представлен в виде 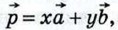 где х и у — некоторые числа, то говорят, что вектор
где х и у — некоторые числа, то говорят, что вектор