|
|
|
|
|
Глава X. Метод координат Дополнительные задачи к главе X. Метод координат (продолжение)1000. Выясните, какие из данных уравнений являются уравнениями окружности. Найдите координаты центра и радиус каждой окружности: а) (х - 1)2 + (y + 2)2 = 25;
1001. Напишите уравнение окружности, проходящей через точки А (3; 0) и В (-1; 2), если центр её лежит на прямой у = х + 2. 1002. Напишите уравнение окружности, проходящей через три данные точки: а) А (1;-4), В (4; 5), С(3;-2);
1003. Вершины треугольника АВС имеют координаты А (-7; 5), В (3; -1), С (5; 3). Составьте уравнения: а) серединных перпендикуляров к сторонам треугольника; б) прямых АВ, ВС и СА; в) прямых, на которых лежат средние линии треугольника. 1004. Докажите, что прямые, заданные уравнениями 3х - 1,5y + 1 = 0 и 2х - у - 3 = 0, параллельны. 1005. Докажите, что точки А, В и С лежат на одной прямой, если: а) А (-2; 0), в) А (1; 2), В (2; 5), С (-10; -31). Применение метода координат к решению задач1006. Две стороны треугольника равны 17 см и 28 см, а высота, проведённая к большей из них, равна 15 см. Найдите медианы треугольника. 1007. Докажите, что отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований. 1008. Дан параллелограмм ABCD. Докажите, что для всех точек М величина (AM2 + СМ2) - (ВМ2 + DM2) имеет одно и то же значение. 1009. Докажите, что медиану АА1 треугольника АВС можно вычислить по формуле 1010. Даны две точки А та В. Найдите множество всех точек М, для каждой из которых: а) 2AM2 - ВМ2 = 2АВ2; б) 2 AM2 + 2ВМ2 = 6 АВ2.
|
|
|



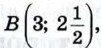 С (6; 4); б) А (3; 10), В (3; 12), С (3; -6);
С (6; 4); б) А (3; 10), В (3; 12), С (3; -6);
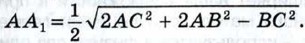 Используя эту формулу, докажите, что если две медианы треугольника равны, то треугольник равнобедренный.
Используя эту формулу, докажите, что если две медианы треугольника равны, то треугольник равнобедренный.