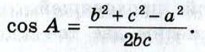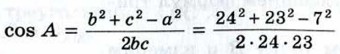Решение треугольников (окончание)

Решение треугольника по трём сторонам

Задача 3

Дано: а, b и с. Найти: ∠A, ∠B и ∠C.

Решение

1. По теореме косинусов получаем:

Угол А находим с помощью микрокалькулятора или по таблице.

2. Аналогично находим угол В.

3. ∠C = 180° - ∠A - ∠B.

Пример

Футбольный мяч находится в точке А футбольного поля на расстояниях 23 м и 24 м от оснований В и С стоек ворот (рис. 294). Футболист направляет мяч в ворота. Найдите угол α попадания мяча в ворота, если ширина ворот равна 7 м.

Рис. 294

Решение

Рассмотрим треугольник АВС, вершинами которого являются точка А расположения мяча и точки В и С в основаниях стоек ворот. По условию задачи с = АВ = 23 м, b = АС = 24 м и а = ВС= 7 м. Эти данные позволяют решить треугольник АВС и найти угол α, равный углу А (см. задачу 3). С помощью теоремы косинусов определяем cos А:

Угол α находим по таблице: α ≈ 16°57'.

<<< К началу