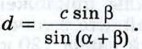|
|
|
|
|
§ 2. Соотношения между сторонами и углами треугольника Измерительные работы (окончание)Измерение расстояния до недоступной точки.Предположим, что нам надо найти расстояние d от пункта А до недоступного пункта С (рис. 296). Напомним, что эту задачу мы уже решали в 8 классе с помощью признаков подобия треугольников. Рассмотрим теперь другой способ решения задачи — с использованием формул тригонометрии.
На местности выберем точку В и измерим длину с отрезка АВ. Затем измерим, например с помощью астролябии, углы А и В: ∠A = α и ∠В = β. Эти данные, т. е. с, α и β позволяют решить треугольник АВС и найти искомое расстояние d = АС. Сначала находим ∠C и sin С: ∠C = 180° - α - β,
Затем с помощью теоремы синусов находим d. Так как Аналогичным образом по так называемому параллаксу небесных светил определяют расстояния до этих светил.
|
|
|




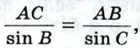 AC = d, АВ = с, ∠B = β, то
AC = d, АВ = с, ∠B = β, то