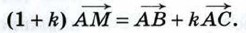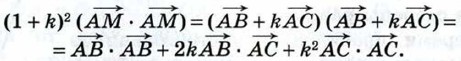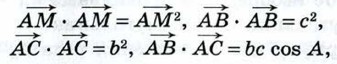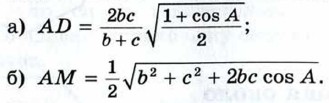|
|
|
|
|
Глава XI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов Дополнительные задачи к главе XI (продолжение)Применение скалярного произведения векторов к решению задач1073. Четырёхугольник ABCD задан координатами своих вершин: А (-1; 2), В (1; -2), С (2; 0), D (1; 6). Докажите, что ABCD — трапеция, и найдите её площадь. Решение Векторы 1074. Точка М лежит на стороне ВС треугольника АВС и ВМ = kMC. Докажите, что (1 + k)2 AM2 = k2b2 + 2bck cos A + c2, где b = AC, с = AB. Решение По условию задачи М лежит на отрезке ВС и ВМ = kMC, поэтому
По правилу треугольника сложения векторов
Отсюда получаем:
Так как
то полученная формула совпадает с искомой формулой. 1075. В треугольнике АВС отрезок AD — биссектриса, AM — медиана, b = АС, с = АВ. Докажите, что:
1076. Диагонали параллелограмма взаимно перпендикулярны. Докажите, что этот параллелограмм является ромбом. 1077. Докажите, что коэффициент подобия двух подобных треугольников равен отношению радиусов окружностей: а) описанных около треугольников; б) вписанных в эти треугольники.
|
|
|



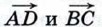 имеют координаты:
имеют координаты: 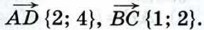 Эти векторы коллинеарны, так как их координаты пропорциональны. По координатам векторов
Эти векторы коллинеарны, так как их координаты пропорциональны. По координатам векторов 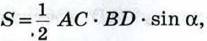 где α — угол между АС и ВО. По формуле (5) § 3 найдём сначала
где α — угол между АС и ВО. По формуле (5) § 3 найдём сначала 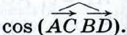 Так как
Так как 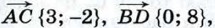 то АС = у√13, BD = 8 и
то АС = у√13, BD = 8 и 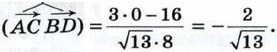 Отсюда следует, что
Отсюда следует, что 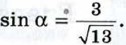 Таким образом,
Таким образом, 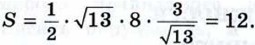
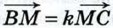 или
или 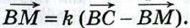 Следовательно,
Следовательно,
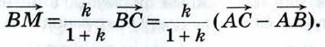
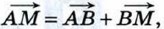 или
или 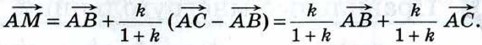 Таким образом,
Таким образом,