|
|
|
|
|
§ 2. Тела и поверхности вращения Задачи к § 2. Тела и поверхности вращения (продолжение)1220. Пусть h, r и V — соответственно высота, радиус основания и объём конуса. Найдите: а) V, если h = 3 см, r = 1,5 см; б) h, если r = 4 см, V=48 π cм3; в) r, если h = m, V = p. 1221. Найдите объём конуса, если площадь его основания равна Q, а площадь боковой поверхности равна Р. 1222. Площадь полной поверхности конуса равна 45л дм2. Развёртка боковой поверхности конуса представляет собой круговой сектор с дугой в 60°. Найдите объём конуса. 1223. Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площади боковой и полной поверхностей образованного при этом вращении конуса. 1224.* Докажите, что объём шара радиуса R равен Решение Рассмотрим два тела: половину шара радиуса R и тело Т, представляющее собой цилиндр радиуса R с высотой R, из которого вырезан конус с радиусом основания и высотой R. Представим себе, что оба тела «стоят» на плоскости а так, как показано на рисунке 368. Проведём секущую плоскость β, параллельную плоскости α и пересекающую радиус шара ОА, перпендикулярный к плоскости α, в точке А1, а высоту ВН конуса — в точке В1. Сечение половины шара представляет собой круг радиуса
Сечение тела Т представляет собой кольцо, площадь которого равна разности площадей двух кругов: круга радиуса R и круга радиуса В1В2 (см. рис. 368), т. е. равна Таким образом, площадь сечения половины шара равна площади сечения тела Т. Поэтому и объём половины шара равен объёму этого тела. В свою очередь, объём V тела Т можно вычислить как разность объёмов цилиндра и конуса:
Итак, объём половины шара равен 1223. Сферу радиуса R покрасили слоем краски толщины d. Слоем такой же толщины покрасили многоугольник и затратили при этом такое же количество краски. Найдите площадь многоугольника. Решение Если толщина слоя краски равна d, то объём краски, затраченной на покраску сферы, равен разности объёмов двух шаров: шара радиуса R + d и шара радиуса R, т. е. равен
При покраске многоугольника площади S слоем толщины d объём затраченной краски равен Sd, поскольку объём призмы равен произведению площади основания на высоту. Приравнивая эти два объёма и сокращая на d, находим S:
Замечание Если толщина d слоя краски очень мала по сравнению с радиусом R сферы, то величина S приблизительно равна
|
|
|



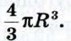
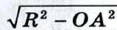 (см. рис. 368). Поэтому площадь этого круга равна π (R2 - OA2).
(см. рис. 368). Поэтому площадь этого круга равна π (R2 - OA2).

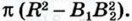 Но В1В2 = ВВ1 (объясните почему) и, кроме того, ВВ1 = ОА1 (доказательство этого наглядно очевидного факта будет приведено в курсе стереометрии 10—11 классов).
Но В1В2 = ВВ1 (объясните почему) и, кроме того, ВВ1 = ОА1 (доказательство этого наглядно очевидного факта будет приведено в курсе стереометрии 10—11 классов).
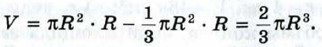
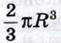 и, следовательно, объём всего шара равен
и, следовательно, объём всего шара равен 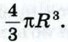
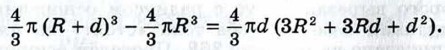
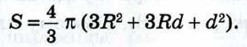
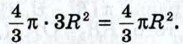 Основываясь на проведённых рассуждениях, естественно принять за площадь сферы величину 4πR2.
Основываясь на проведённых рассуждениях, естественно принять за площадь сферы величину 4πR2.