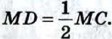|
|
|
|
|
Задачи повышенной трудности Ответы к задачам повышенной трудности: Глава III. Параллельные прямые и Глава IV. Соотношения между сторонами и углами треугольника333. 335. а) Остроугольный; б) остроугольный. 336. Указание. Воспользоваться соотношениями между сторонами и углами треугольника и теоремой о сумме углов треугольника. 337. 70°. Указание. Пусть О — точка пересечения биссектрисы угла А и прямой ВМ. Сначала доказать равенство треугольников АОС и МОС. 338. Указание. Соединить один из концов отрезка с вершиной треугольника и воспользоваться задачей 312. 339. Указание. Воспользоваться задачей 173, а также соотношениями между сторонами и углами треугольника. 340. Указание. Продолжить отрезок AD до пересечения с ВС и воспользоваться задачей 312. 341. Указание. Отметить на стороне АВ такую точку С1, что АС1 = АС, и рассмотреть треугольник BC1D. 342. Указание. Доказать методом от противного. 343. Указание. Пусть АВС — данный треугольник, АВ > ВС, ВМ — медиана. Отметить такую точку Е, что М является серединой отрезка BE, и рассмотреть треугольник АВЕ. 344. Указание. Воспользоваться задачей 173. 345. Указание. Продолжить отрезок В А на отрезок AD = АС и, рассмотрев 346. Указание. Воспользоваться задачей 341. 347. Указание. Воспользоваться задачами 343 и 346. 349. Указание. Пусть в треугольнике АВС медиана AM и высота АН делят угол А на три равных угла ВАН, НАМ и MAC. Провести перпендикуляр MD к стороне АС и доказать сначала, что 350. Указание. Учесть, что в прямоугольном треугольнике гипотенуза больше катета. 352. Нет. Указание. Воспользоваться задачей 160. 353. Два, одно или ни одного. Указание. Воспользоваться задачей 160. 354. Задача имеет одно решение, если данные точки не лежат на одной прямой, и не имеет решения, если эти точки лежат на одной прямой. Указание. Воспользоваться задачей 160. 355. Указание. Сначала построить такую точку А1, что прямая а проходит через середину отрезка АА1 перпендикулярно к нему, а затем провести отрезок А1В. 357. Четыре, три, два, одно или ни одного. Указание. Воспользоваться задачей 311. 358. Четыре. Указание. Воспользоваться задачей 311. 359. Указание. Сначала построить треугольник OAD, в котором AD = R и OD = 2R, где R — радиус данной окружности. 360. Указание. Пусть даны острый угол А, высота ВН искомого треугольника АВС и отрезок PQ, равный его периметру. Построить сначала 361. Указание. Построить сначала треугольник, у которого сторона равна данному периметру, а углы, прилежащие к ней, равны половинам данных углов. 362. Указание. Пусть ВС, АС + АВ, ∠B - ∠C — данные элементы искомого треугольника АВС. На продолжении стороны СА за точку А отложить отрезок АА1, равный отрезку АВ. Построить сначала
|
|
|



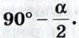
 DHB, воспользоваться неравенством треугольника.
DHB, воспользоваться неравенством треугольника.