|
|
|
|
|
§ 1. Площадь многоугольника Площадь квадратаДокажем, что площадь S квадрата со стороной а равна а2. Начнём с того случая, когда
Пусть теперь число а представляет собой конечную десятичную дробь, содержащую п знаков после запятой (в частности, число а может быть целым, и тогда n = 0). Тогда число m + а • 10n Целое. Разобьём данный квадрат со стороной а на m2 равных квадратов так, как показано на рисунке 180, б (на этом рисунке m = 7).
При этом каждая сторона данного квадрата разобьётся на m равных частей, и, значит, сторона любого маленького квадрата равна
По формуле (1) площадь маленького квадрата равна
Наконец, пусть число а представляет собой бесконечную десятичную дробь. Рассмотрим число ап, получаемое из а отбрасыванием всех десятичных знаков после запятой, начиная с (n + 1)-го. Так как число а отличается от аn не более чем на
Ясно, что площадь S данного квадрата заключена между площадью квадрата со стороной аn и площадью квадрата со стороной
Будем неограниченно увеличивать число n. Тогда число
|
|
|



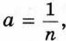 где n — целое число. Возьмём квадрат со стороной 1 и разобьём его на n2 равных квадратов так, как показано на рисунке 180, а (на этом рисунке n = 5). Так как площадь большого квадрата равна 1, то площадь каждого маленького квадрата равна
где n — целое число. Возьмём квадрат со стороной 1 и разобьём его на n2 равных квадратов так, как показано на рисунке 180, а (на этом рисунке n = 5). Так как площадь большого квадрата равна 1, то площадь каждого маленького квадрата равна 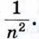 Сторона каждого маленького квадрата равна
Сторона каждого маленького квадрата равна 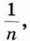 равна а. Итак,
равна а. Итак,
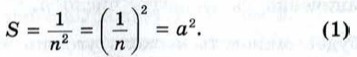

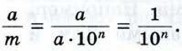
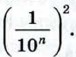 Следовательно, площадь S данного квадрата равна
Следовательно, площадь S данного квадрата равна
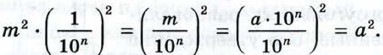
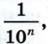 то
то 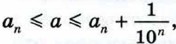 откуда
откуда
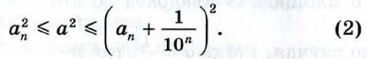
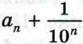 (рис. 180, в), т. е. между
(рис. 180, в), т. е. между 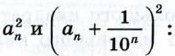
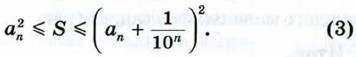
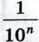 будет становиться сколь угодно малым, и, значит, число
будет становиться сколь угодно малым, и, значит, число 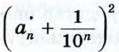 будет сколь угодно мало отличаться от числа
будет сколь угодно мало отличаться от числа 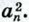 Поэтому из неравенств (2) и (3) следует, что число S сколь угодно мало отличается от числа а2. Следовательно, эти числа равны: S = a2, что и требовалось доказать.
Поэтому из неравенств (2) и (3) следует, что число S сколь угодно мало отличается от числа а2. Следовательно, эти числа равны: S = a2, что и требовалось доказать.