|
|
|
|
|
§ 1. Рациональные дроби и их свойства Рациональные выражения
17. а) При любом значении х: х2 ≥ 0; х2 + 1 ≥ 1; значит б) При любом значении у: у2 ≥ 0; у2 + 4 ≥ 4; в) При любом значении а: (а - 1)2 ≥ 0; а2 + 10 > 0; значит г) При любом значении b: (b - 3)2 ≥ 0; b2 + 1 > 0; -b2 - 1 < 0; значит 18. а) Очевидно, что а2 + 5 ≥ 5. Причем а2 + 5 = 5 при а = 0; Наибольшее значение б) Очевидно что (а - 3)2 + 1 ≥ 1. Причем (а - 3)2 + 1 = 1 при а = 3; Наибольшее значение 19. а) b2 + 7 ≥ 7. Причем b2 + 7 = 7 при b = 0; Наименьшее значение б) (b - 2)2 + 16 ≥ 16. Причем (b - 2)2 + 16 = 16 при b = 2; Наименьшее значение 20. 21. а) (2а + 3) (2а - 3) = 4а2 - 9; б) (у - 5b) (у + 5b) = у2 - 25b; в) (0,8x + у)(у - 0,8а;) = у2 - 0,64х2; г) (b + 0,5)2 = b2 + b + 0,25; д) (а - 2х)2 = а2 - 4ах + 4х2; е) (ab - 1)2 = а2b2 - 2аb + 1. 22. a) x2 -25 = (x - 5)(x + 5); 6) 16 - c2 = (4 - c)(4 + c); в) a2 - 6a + 9 = (a - 3)2; г) x2 + 8x + 16 = (x + 4)2; д) a3 - 8 = (a - 2)(a2 + 2a + 4); e) b3 + 27 = (b + 3)(b2 - 3b + 9).
|
|
|



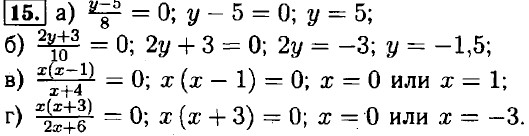
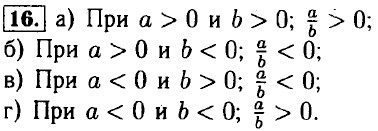
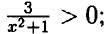
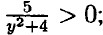 значит
значит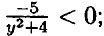

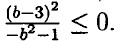
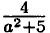 при а = 0.
при а = 0.
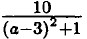 при а = 3.
при а = 3.
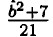 при b = 0.
при b = 0.
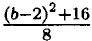 При b = 2.
При b = 2.
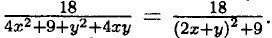 Максимальное значение при (2х + у)2 = 0.
Максимальное значение при (2х + у)2 = 0. 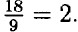 Ответ: 3. Равно 2.
Ответ: 3. Равно 2.