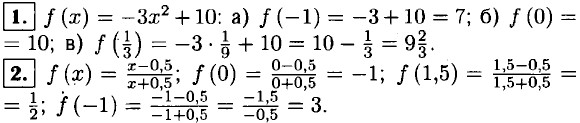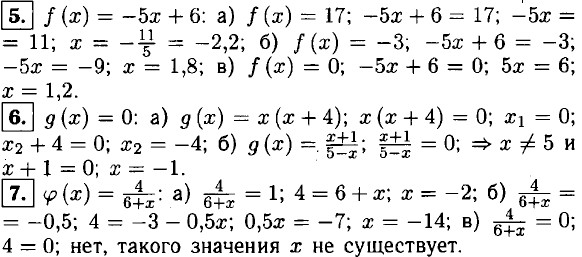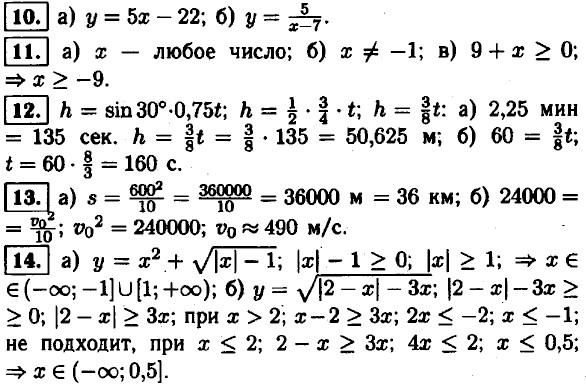Функция. Область определения и область значений функций

3. ƒ(x) = x³ - 10: а) ƒ(5) = 5³ - 10 = 125 - 10 = 115; б) ƒ(4) = 4³ - 10 = 64 - 10 = 54; в) ƒ(2) = 2³ - 10 = 8 - 10 = -2; г) ƒ(-3) = (-3)³ - 10 = -27 - 10 = -37.

4. φ(x) = x² + x + 1; φ(0) = 0 + 0 + 1 = 1; φ(1) = 1 + 1 + 1 = 3; φ(2) = 4 + 2 + 1 = 7; φ(3) = 9 + 3 + 1 = 13; ⇒ φ(0) + φ(1) + φ(2) + φ(3) = 1 + 3 + 7 + 13 = 24.

8. ƒ(x) = 0,5x - 4; а) 0,5x - 4 = -5; 0,5x = -1; x = -2; 0) 0,5x -4 = 0; 0,5x = 4; x = 8; в) 0,5x - 4 = 2,5; 0,5x = 6,5; x = 13.

9. а) x — любое число; б) x — любое число; в) x ≠ 5; г) x ≠ 4 и x ≠ -1; д) x² + 1 > 0; ⇒ x — любое число; е) x - 5 ≥ 0; x ≥ 5.

15. а) g(-4) = -3; g(-1) = -2; g(1) = 3; g(5) = 3;

б) g(1,5) = g(4,5) = 4; g(-3) = -4; g(-6) = g(0) = 0; в) наибольшее значение функции 6, наименьшее значение функции -4; г) область значений функции [-4; 6].

16. а) Атмосферно давление 5 марта было 750 мм рт. ст. 9 марта 752 мм рт. ст.; б) Атмосферное давление было наибольшим 4 марта.

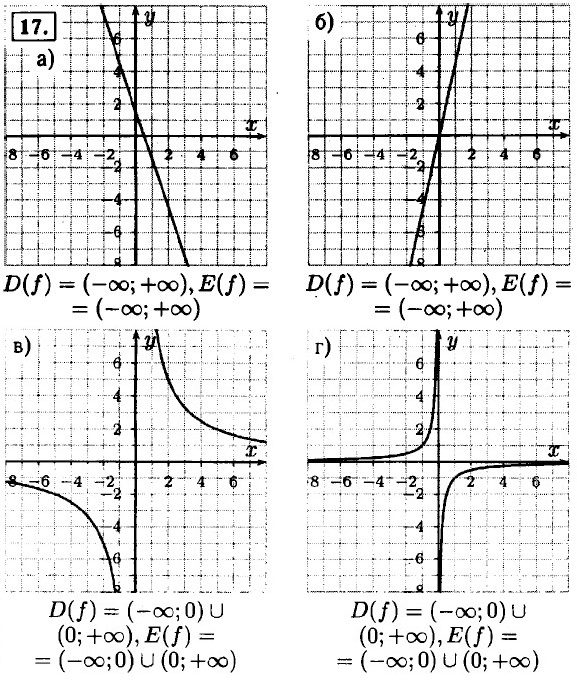
18. а) ƒ(х) = 2х - 1 — график линейной функции, 1 ≤ х ≤ 4; ƒ(1) = 2 - 1 = 1; ƒ(4) = 8 - 1 = 7; область определения [1; 7]; б) g(х) = -3х + 8 — график линейной функции, -2 ≤ х ≤ 5; g(-2) = 6 + 8 = 14; g(5) = -15 + 8 = -7; область определения [-7; 14].

19. у = х²; область определения и область значения (-∞; +∞). у = х³; область определения и область значения (-∞; +∞). у = √х; область определения и область значения (0; +∞).

Окончание >>>