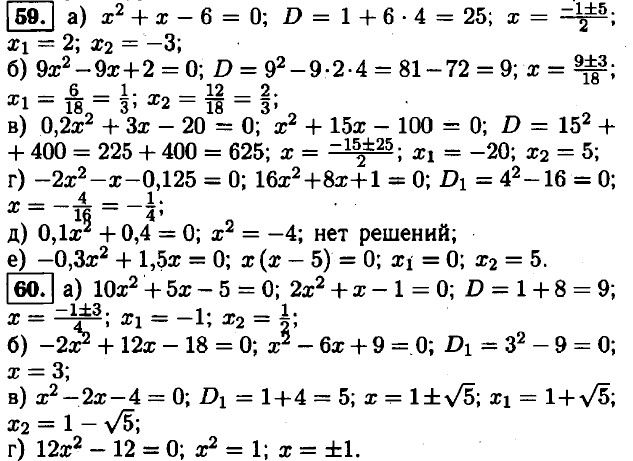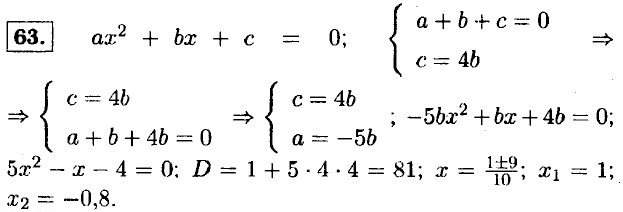Квадратный трехчлен и его корни

55. х = {-2; 2; 3}.

56. а) х² - 7х = 0; х (х - 7) = 0; х₁ = 0; х₂ = 7;

б) 2х - 5 = 0; 2х = 5; х = 2,5;

в) у³ - 4у = 0; у(у² - 4) = 0; ⇒ x₁ = 0; у² - 4 = 0; у² = 4; ⇒ y₁ = 0; у₂ = -2; у₃ = 2;

г) у⁴ - 16 = 0; у⁴ = 16; у = ±2

57. а) нет; б) да; в) нет; г) нет.

58. х² - 6х + 7 = 0; D₁ = 3² - 7 = 9 - 7 = 2; х = 3 ± √2; ⇒ корнем уравнения является 3 - √2.

61. а) 5х² - 8х + 3 = 0; D₁ = 4² - 5 • 3 = 16 - 15 = 1 > 0; уравнение имеет два корня;

б) 9х² + 6х + 1 = 0; D₁ = 3² - 9 = 0; уравнение имеет один корень; в) -7х² + 6х - 2 = 0; D₁ = 3² - 7 • 2 = 9 - 14 = -5 < 0; уравнение не имеет корней;

г) -х² + 5х - 3 = 0; D = 25 - 4 • 3 = = 25 - 12 = 13 > 0; уравнение имеет два корня.

62. а) -4х² - 4х + 3 = 0; D₁ = 2² + 4 • 3 = 4 + 12 = 16 > 0; уравнение имеет два корня;

б) 4х² - 4х + 3 = 0; D₁ = 2² - 3 • 4 = 4 - 12 = -8 < 0; уравнение не имеет корней;

в) 9х² - 12х + 4 = 0; D₁ = 6² - 4 • 9 = 36 - 36 = 0; уравнение имеет один корень;

г) 9х² - 12х • 4 = 0; D₁ = 6² + 4 • 9 = 36 + 36 = 72 > 0; уравнение имеет два корня.

Окончание >>>