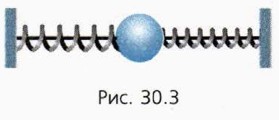
§ 30. Потенциальная энергия (окончание)

ПОВЫШЕННЫЙ УРОВЕНЬ

7. С башни высотой 20 м брошен горизонтально камень массой 200 г с начальной скоростью 10 м/с. Чему равны через 1 с после начала движения:

а) кинетическая энергия камня?

б) потенциальная энергия камня относительно земли?

8. К пружине подвешен груз массой 5 кг. Чему равна потенциальная энергия упругой деформации пружины, если удлинение пружины равно 2 см?

9. Чтобы сжать недеформированную пружину на 4 см, надо приложить силу 40 Н. Насколько увеличится потенциальная энергия пружины, если сжать её ещё на 2 см?

10. К пружине подвешены два одинаковых груза. Один из грузов снимают. На сколько процентов уменьшится потенциальная энергия пружины, когда оставшийся груз будет находиться в покое?

ВЫСОКИЙ УРОВЕНЬ

11. К пружине, закреплённой верхним концом, подвешивают груз и медленно опускают его до положения равновесия. Чему равно отношение изменения потенциальной энергии груза к изменению потенциальной энергии пружины?

12. Две пружины жёсткостью 400 Н/м и 1 кН/м соединены, как показано на рисунке 30.3. В начальном положении пружины не деформированы. Чему будет равна потенциальная энергия системы пружин, если сместить шар на 3 см?

Рис. 30.3

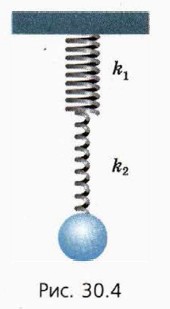
13. К центру горизонтального гладкого диска, вращающегося вокруг вертикальной оси, прикреплена пружина, на другом конце которой закреплён груз массой m. Ось вращения проходит через центр диска. Жёсткость пружины k. Длина пружины в недеформированном состоянии l₀. Груз вращается в горизонтальной плоскости с угловой скоростью ω. Чему равна потенциальная энергия пружины?

14. К нижнему концу пружины жёсткостью k₁ присоединена другая пружина жёсткостью k₂, к которой прикреплён груз (рис. 30.4). Чему равно отношение потенциальных энергий пружин?

Рис. 30.4

<<< К началу Ответы >>>