|
|
|
|
|
Удельная теплоемкость. Уравнение теплового баланса Удельная теплоемкость. Уравнение теплового баланса: Ответы, указания, решения4.5. У медной. 4.13. На нагревание воды. 4.14. Из-за большой удельной теплоемкости воды. 4.15. 25,2 кДж. 4.16. 24 г. 4.17. 4.18. 420 °С. 4.19. 60 °С. 4.20. На 75 °С. 4.21. Если опустить алюминиевую ложку. 4.22. Главная причина — масса кирпичной печи намного больше, чем железной. 4.23. После дождя в почве много воды, у которой большая удельная теплоемкость. Кроме того, при испарении происходит охлаждение почвы. 4.27. Малой удельной теплоемкостью песка. 4.28. 1,2 МДж. 4.29. 720 кДж. 4.30. 50 °С. Решение. В теплопередаче участвуют два тела: холодная вода получает количество теплоты Q1 = cm1(t - t1), кипяток отдает количество теплоты Q2 = cm2(t2 - t). Здесь с — удельная теплоемкость воды, t = 100 °С. Согласно уравнению теплового баланса Q1 = Q2. Следовательно, cm1(t - t1) = cm2(t2 - t), откуда
4.31. 0,5 кг. 4.32. Ha 5 km. 4.33. 1,5 л. 4.34. 60 °C. 4.35. 4.36. 4.37. Например, из меди. 4.38. В 9 раз. 4.39. Например, из алюминия. 4.40. На 5 °С. Решение. Для подъема ртути массой m на высоту h надо затратить энергию Е = mgh. Чтобы нагреть эту ртуть на Δt, надо сообщить ей количество теплоты Q = cm • Δt, где с — удельная теплоемкость ртути. Поскольку Q = Е, получаем 4.41. На 1,2 °С. 4.42. 42 км. 4.43. На 3,6 °С. 4.44. На 25 м. 4.46. 15 °С. 4.47. 85 кг холодной воды и 65 кг горячей. 4.48. 25 кг и 75 кг. 4.49. 19,5 °С. 4.50. 55 °С. 4.51. 14 %. 4.52. Для нагревания воздуха; в 1,8 раза. 4.53. На 43 °С. 4.54. На 12 °С. 4.55. Стального. 4.56. Алюминиевый. 4.57. 2,5 кг воды; со ртутью. 4.58. За 4 с. 4.59. 47 %. 4.60. На 2 °С. Указание. Предположите, что за указанное время каждую секунду вода отдавала одно и то же количество теплоты. Проверьте затем, подтверждает ли полученный ответ это предположение. 4.61. Решение. Обозначим массы шарика и воды соответственно m и mв, а удельные теплоемкости с и св, температуру после переноса N шариков tN. Температура кипятка t0 = 100 °С. Согласно уравнению теплового баланса cвmв(tN - tв) = Ncm(t0 - tN). Если N = 1, получим cвmв(t1 - tв) = cm(t0 - t1). Подставив в это уравнение числовые значения известных величин, получим свтв = 3cm. Тогда при любом N справедливо уравнение 3(tN - tв) = N(t0 - tN). Отсюда 4.62. Указание. Молоко и воду можно, например, разлить в сосуды вместимостью по 0,5 л и затем осуществлять теплопередачу между этими сосудами.
|
|
|



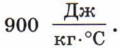
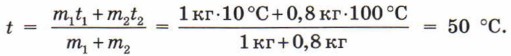
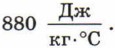
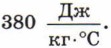
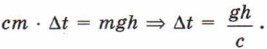
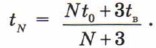 После переноса второго и третьего шариков температура в калориметре будет соответственно 52 и 60 °С. Подставив значение tN = 90 °С, получим N = 21.
После переноса второго и третьего шариков температура в калориметре будет соответственно 52 и 60 °С. Подставив значение tN = 90 °С, получим N = 21.