Двоичное кодирование числовой информации

Известно множество способов записи чисел. Мы пользуемся десятичной позиционной системой счисления.

Десятичной она называется потому, что в этой системе счисления десять единиц одного разряда составляют одну единицу следующего старшего разряда. Число 10 называется основанием десятичной системы счисления. Для записи чисел в десятичной системе счисления используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Позиционной эта система счисления называется потому, что одна и та же цифра получает различные количественные значения в зависимости от места, или позиции, которую она занимает в записи числа. Например, в записи числа 555 цифра 5, стоящая на первом месте справа, обозначает 5 единиц, на втором — 5 десятков, на третьем — 5 сотен.

Рассмотрим два числовых ряда:

1, 10, 100, 1000, 10 000, 100 000 ...
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 ...

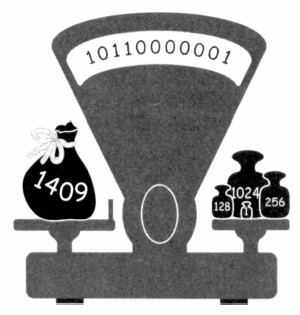
Оба этих ряда начинаются с единицы. Каждое следующее число первого ряда получается путем умножения предыдущего числа на 10. Каждое следующее число второго ряда получается путем умножения предыдущего числа на 2.

Любое целое число можно представить в виде суммы разрядных слагаемых — единиц, десятков, сотен, тысяч и так далее, записанных в первом ряду. При этом каждый член этого ряда может либо не входить в сумму, либо входить в нее от 1 до 9 раз. Пример:

1409 = 1 • 1000 + 4 • 100 + 0 • 10 + 9 • 1.

Числа 1, 4, 0, 9, на которые умножаются члены первого ряда, составляют исходное число 1409.

Перевод целых десятичных чисел в двоичный код

Способ 1

Попробуем представить число 1409 в виде суммы членов второго ряда.

Воспользуемся методом разностей. Возьмем ближайший к исходному числу, но не превосходящий его член второго ряда и составим разность:

1409 - 1024 = 385.

Возьмем ближайший к полученной разности, но не превосходящий ее член второго ряда и составим разность:

385 - 256 = 129.

Аналогично составим разность:

129 - 128 = 1.

В итоге получим:

1409 = 1024 + 256 + 128 + 1 = 1 • 1024 + 0 • 512 +
+ 1 • 256 + 1 • 128 + 0 • 64 + 0 • 32 + 0 • 16 +
+ 0 • 8 + 0 • 4 + 0 • 2 + 1 • 1.

Мы видим, что каждый член второго ряда может либо не входить в сумму, либо входить в нее только один раз.

Числа 1 и 0, на которые умножаются члены второго ряда, также составляют исходное число 1409, но в его другой, двоичной записи: 10110000001.

Результат записывают так:

1409₁₀ = 10110000001₂.

Исходное число мы записали с помощью 0 и 1, другими словами, получили двоичный код этого числа, или представили число в двоичной системе счисления.

Окончание >>>