13.1. Представление целых чисел

В прямом коде числа можно хранить, но выполнение арифметических операций над числами в прямом коде затруднено — оно требует более сложной архитектуры центрального процессора, «умеющего» выполнять не только сложение, но и вычитание, а также «знающего» особый алгоритм обработки не имеющего «веса» знакового разряда. Этих трудностей позволяет избежать использование дополнительного кода.

Чтобы понять сущность дополнительного кода, рассмотрим работу реверсивного счётчика, последовательность показаний которого можно представить в виде замкнутого кольца из чисел (рис. 3.5).

Реверсивный счётчик

При возрастании показаний счётчика до максимального, например до 999, следующими его состояниями должны быть 1000, 1001, 1002 и т. д. Но для изображения старшей единицы в счётчике не хватает разряда, происходит переполнение разрядной сетки. Поэтому мы увидим 000, 001, 002 и т. д.

При убывании показаний счётчика после состояния 000 будут идти 999, 998, 997 и т. д. Но после достижения нуля последовательное вычитание единицы должно давать -1, -2, -3 и т. д.

Будем рассматривать числа 999, 998, 997 как коды чисел -1, -2, -3 и проверим на их примере соотношение: у + (-у) = 0:

001 + 999 = 1000;
002 + 998 = 1000;
003 + 997 = 1000.

С учётом того что единица переполнения теряется, мы, сложив число и код противоположного ему числа, получаем ноль!

Вот ещё несколько примеров:

5 - 2 = 5 + [-2] = 5 + 998 = 1003;
7 - 5 = 7 + [-5] = 7 + 995 = 1002.

Для устранения неоднозначности в кольце будем считать половину состояний (0-499) кодами нуля и положительных чисел, а оставшуюся половину (500-999) — кодами отрицательных чисел.

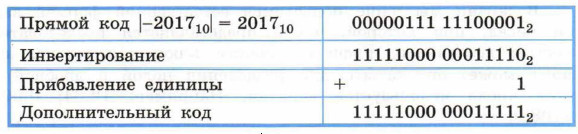
Таким образом, дополнительный код положительного числа совпадает с этим числом, а для отрицательного числа он равен дополнению его величины до числа qⁿ, возникающего при переполнении разрядной сетки. Здесь q — основание системы счисления, n — число разрядов в разрядной сетке.

Рассмотрим алгоритм получения дополнительного n-разрядного кода отрицательного числа:

1) модуль числа представить прямым кодом в n двоичных разрядах;

2) значения всех разрядов инвертировать (все нули заменить единицами, а единицы — нулями);

3) к полученному представлению, рассматриваемому как n-разрядное неотрицательное двоичное число, прибавить единицу.

Пример 1. Найдём 16-разрядный дополнительный код отрицательного числа -2017₁₀.

Использование дополнительного кода позволяет свести операцию вычитания чисел к операции поразрядного сложения кодов этих чисел.

Пример 2. Как известно, 48 - 2017 = -1969.

Выполним эту операцию в 16-разрядных машинных кодах.

Нам потребуются прямой код числа 48 и дополнительный код числа -2017.

Рассмотрим полученный результат. Это отрицательное число (об этом говорит 1 в знаковом разряде), представленное в дополнительном коде. Перейдём к прямому коду модуля соответствующего числа, по которому сможем восстановить десятичное представление результата.

Прямой код можно получить из дополнительного кода, если применить к нему операцию инвертирования и прибавить единицу.

Получаем: -11110110001₂ = -1969.

<<< К началу