|
|
|
|
|
§ 17. Некоторые сведения из теории множеств Операции над множествамиНад множествами, как и над числами, производят некоторые операции.
Пересечение множеств обозначают с помощью знака ∩ : X ∩ Y. На рисунке 4.2 закрашено множество Х ∩ Y.
Пусть множества X и Y состоят из букв: X = {ш, к, о, л, а};
Эти множества имеют общие элементы: к, о. X ∩ Y = {к, о}. Множества М и X не имеют общих элементов, их пересечение — пустое множество: М ∩ Х = ∅. Пересечение множеств М и Р есть множество Р, а пересечение множеств М и М есть множество М: М ∩ Р = Р;
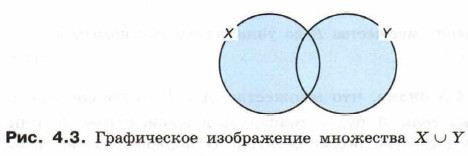
Объединение множеств обозначают с помощью знака ∪: X ∪ Y. На рисунке 4.3 закрашено множество X ∪ Y.
Для наших примеров: X ∪ Y = {ш, к, о, л, а, у, р};
Пересечение и объединение выполняются для любой пары множеств. Третья операция — дополнение — имеет смысл не для всех множеств, а только тогда, когда второе множество является подмножеством первого.
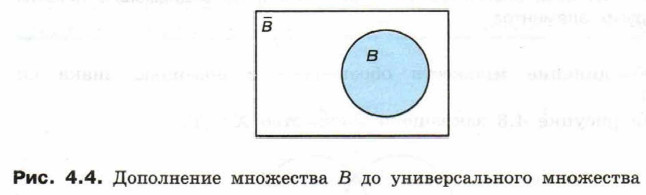
Дополнение Р до М обозначают Дополнение М до М есть пустое множество, дополнение пустого множества до М есть М: Особый интерес представляет дополнение некоторого множества В до универсального множества U. Например, если В — это множество точек, принадлежащих некоторому отрезку, то его дополнением В до универсального множества U, которым в данном случае является множество всех точек числовой прямой, является множество точек, не принадлежащих данному отрезку. В общем случае можем записать:
|
|
|



 Пересечением двух множеств X и Y называется множество их общих элементов.
Пересечением двух множеств X и Y называется множество их общих элементов.

 Подумайте, возможно ли равенство: А ∪ В = А ∩ В.
Подумайте, возможно ли равенство: А ∪ В = А ∩ В.
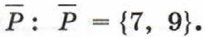
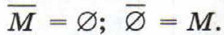
 (рис. 4.4)
(рис. 4.4)